Доведемо, що інших коренів немає. Щоб їх не було, функція має рости (або спадати — тут це неважливо, бо обидві функції непарні) швидше, ніж функція на всій області визначення (тобто її похідна має бути більшою) Знайдемо похідні обох функцій:
Доведемо, що , тобто . Це випливає з того, що (за означенням косинуса), а (доведемо це):
Квадрат виразу не може бути від'ємним на множині дійсних чисел, тому нерівність доведено.
Решение: Узнаем каковы площади этих квадратов: 3части*3 части=9частей² 4части*4части=16части² Сумма частей квадратов: 9+16=25 (частей)² Далее можно решить задачу методом пропорции, зная что 25 частей² равны 100дм², а 9 частей обозначим за (х) дм²-этим мы узнаем площади каждого квадрата: 25 - 100 9 - х х=9*100 : 25=36 (дм²)-площадь первого квадрата 100-36=64 (дм²)-площадь второго квадрата Зная площади каждого квадратов, найдём их стороны: Первого квадрата: а=√36=+-6 а=6 (дм)-сторона первого квадрата Второго квадрата: а=√64=+-8 а=8 (дм)-сторона второго квадрата
Решение: Узнаем каковы площади этих квадратов: 3части*3 части=9частей² 4части*4части=16части² Сумма частей квадратов: 9+16=25 (частей)² Далее можно решить задачу методом пропорции, зная что 25 частей² равны 100дм², а 9 частей обозначим за (х) дм²-этим мы узнаем площади каждого квадрата: 25 - 100 9 - х х=9*100 : 25=36 (дм²)-площадь первого квадрата 100-36=64 (дм²)-площадь второго квадрата Зная площади каждого квадратов, найдём их стороны: Первого квадрата: а=√36=+-6 а=6 (дм)-сторона первого квадрата Второго квадрата: а=√64=+-8 а=8 (дм)-сторона второго квадрата
Перший корінь одразу видно: це 0 (бо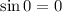 ).
).
Доведемо, що інших коренів немає. Щоб їх не було, функція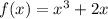 має рости (або спадати — тут це неважливо, бо обидві функції непарні) швидше, ніж функція
має рости (або спадати — тут це неважливо, бо обидві функції непарні) швидше, ніж функція 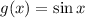 на всій області визначення (тобто її похідна має бути більшою) Знайдемо похідні обох функцій:
на всій області визначення (тобто її похідна має бути більшою) Знайдемо похідні обох функцій:
Доведемо, що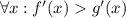 , тобто
, тобто 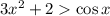 . Це випливає з того, що
. Це випливає з того, що 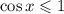 (за означенням косинуса), а
(за означенням косинуса), а 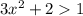 (доведемо це):
(доведемо це):
Квадрат виразу не може бути від'ємним на множині дійсних чисел, тому нерівність доведено.
Відповідь: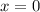 .
.