Работа по теме "Множества и логика"

1) Найти объеденение и пересечение множеств:
P = {-1;0}
Q = {-3; -2; -1; 0; 1}

2) Записать уравнение окружности и прямой, если:

C (-2;4) центр окружности
R = 5

3) На координатной плоскости построить фигуру заданную а) уравнением, б) системой уравнений. В ответе записать, что является этой фигурой.

а) 5х - 2у = 4
б)

4) На координатной плоскости показать множество являющийся решением а) неравенства, б) системы неравенств

а) 3х+2у = - 3

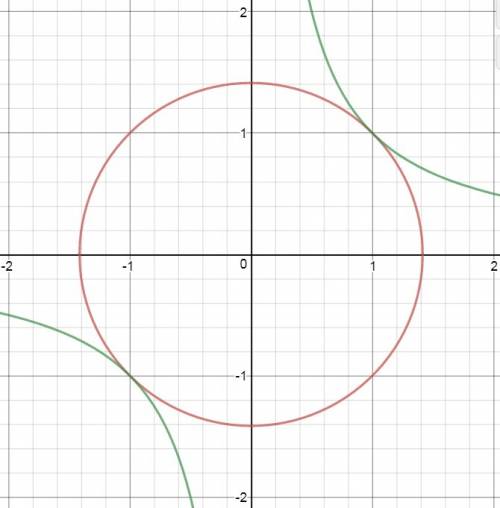
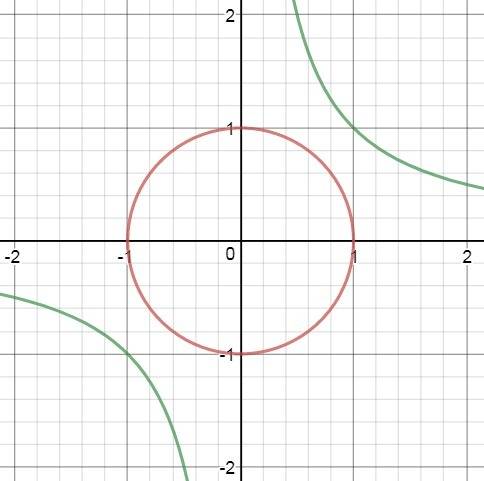
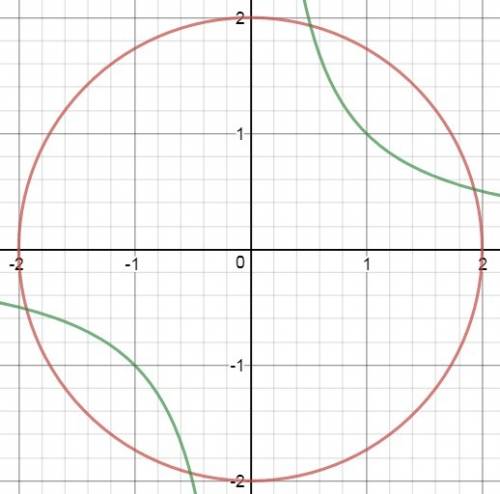
б)
9 }{2x + 3y \leqslant 3} " class="latex-formula" id="TexFormula2" src="https://tex.z-dn.net/?f=%20%5Cbinom%7B%20%7Bx%7D%5E%7B2%7D%20%2B%20%7By%7D%5E%7B2%7D%20%3E%209%20%7D%7B2x%20%2B%203y%20%5Cleqslant%203%7D%20" title=" \binom{ {x}^{2} + {y}^{2} > 9 }{2x + 3y \leqslant 3} ">

👇

Открыть все ответы

Ответ:

иортььо

16.09.2022

Попробуем найти "шаблоны" расстановок цифр, по которым потом можно будет восстановить любое число, подходящее под определение "хорошего". Затем, исходя из них, посчитаем и количество.

Пусть X = от 1 до 9; и Y = от 1 до 9. При этом X не = Y в один и тот же момент. (то есть одни не могут быть равны одному и тому же числу)

Самый простой вариант - все числа повторяются ровно или более 2 раз.

Попытаемся внести новое число в шаблон.
Y - не подходит, так как Y должен повторяться ровно или более двух раз.

YYXXX - подходит. При этом YYYXX бессмысленно, так как охватывает тот же диапазон. Далее двигаться также бесполезно, ибо X не может быть только один, а равносилен .
А вот про то, что положения у Y среди X может быть разный, забывать не стоит. Так что стоит учесть все возможные его расстановки.

Тогда количество шаблонов можно будет вычислить как кол-во перестановок Y в X плюс шаблон .

Формулы комбинаторики не помню (2 к 5 тра-та-та) так что буду решать "на живую": с = (4+3+2+1) = 10 - кол-во перестановок
10+1 = 11 - с учетом шаблона .

Теперь о числах. По сути, их всего два. Так как меняются одни в шаблоне одновременно (меняется значение X, то меняются и все X в шаблоне). Так что можно рассматривать это как число XY, но не простое. Как я говорил выше, X не может = Y. И нулями числа быть не могут. Посчитаем количество подстановок цифр вместо X и Y.

L = 9*8 + 8 = 10*8 = 80 (для каждого из 9 X соответствует 8 значений Y (без совпадения), и остается ещё одно значение Y, рассматривая которое, мы приходим к выводу, что для него также есть 8 значений X)

И каждую из этих 80 комбинаций XY можно подставить в 11 шаблонов, что даст возможность воссоздать любое "хорошее" пятизначное число.

80*11 = 880 - ответ

4,4(13 оценок)

Ответ:

Mila19911

16.09.2022

Начнем с того, что выражение x²+y²≥0 при любых x и y, значит отрицательные значения a мы не рассматриваем.

Первое уравнение системы:
x²+y²=a
это уравнение окружности с центром в начале координат. Значение a задает радиус окружности.

Второе уравнение системы:
xy=1
это гипербола y=1/x, лежащая в 1 и 3 координатных четвертях. Самые близкие к началу координат точки, принадлежащие этому графику - (1;1)
и (-1;-1)

Рассмотрим три случая:
1)
a таково, что окружность проходит через точки (-1;-1) и (1;1), следовательно система имеет 2 решения. Найдем a.
По теореме Пифагора из прямоугольного треугольника с катетами равными 1, гипотенуза=радиус=√(1²+1²)=√2 ⇒ a=√2²=2
При a=2 система имеет 2 решения

2)
а таково, что окружность не пересекает гиперболу y=1/x. это произойдет в том случае, если радиус меньше двух.
При a∈[0;2) система не имеет решений

3)
а таково, что окружность пересекает гиперболу в 4 точках. это произойдет, если радиус больше двух.
При a∈(2;+∞) система имеет 4 решения

Графики для каждого случая приложены для наглядности.
Сколько решений имеет система уравнений х2+y2=а ,xy=1 при различных параметрах а?