2х²+4y²-2x+4xy+1=0;
(4y²+4xy+x²)+(x²-2x+1)=0;
(2y+x)²+(x-1)²=0;
{ 2y+x=0;
{ x-1=0;
y=-1/2;
x=1.
ответ: (1; -1/2).
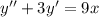
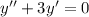
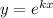 , тогда подставив в однородное уравнение, получаем характеристическое уравнение
, тогда подставив в однородное уравнение, получаем характеристическое уравнение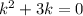
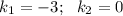
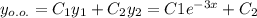
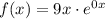 отсюда
отсюда 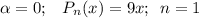
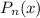 - многочлен степени х
- многочлен степени х с корнями характеристического уравнения и, принимая во внимания что n=1 , частное решение будем искать в виде:
с корнями характеристического уравнения и, принимая во внимания что n=1 , частное решение будем искать в виде: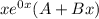
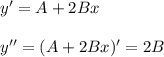
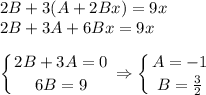
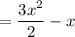
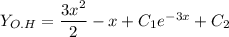 - ответ
- ответ
x^2+x^2+4y^2-2x+4xy+1=0
Группируем по 3 члена
(x^2+4xy+4y^2)+(x^2-2x+1)=0
В скобках ФСУ квадрат суммы, собираем
(x+2y)^2+(x-1)^2=0
Сумма квадратов равна 0, если каждое слагаемое расно 0. Приравниваем каждое слагаемое к 0 и объединяем наши получившиеся уоавнения системой
Система:
x+2y=0
x-1=0
Решение системы:
x-1=0
x=1
1+2y=0
2y=-1
y=-1/2
ответ:(1; -1/2)