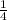 (y-0,4)=2,25
(y-0,4)=2,25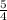 y -
y - 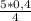 = 2,25
= 2,25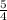 y = 2,25 +
y = 2,25 + 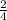
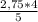
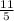
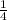 - m)/1,2 = 0,24
- m)/1,2 = 0,24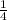 - m = 0,24 * 1,2
- m = 0,24 * 1,2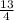
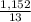
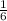 = 2
= 2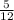
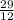 -
- 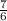
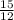
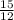 /5
/5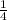 ⇔ x = 0,25
⇔ x = 0,25 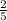 z+
z+ ) = 4,2
) = 4,2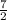 ·
·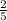 z +
z +  ·
·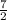 = 4,2
= 4,2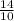 z +
z + 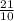 = 4,2
= 4,2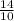 z =
z = 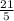 -
- 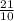
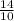 z =
z = 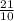
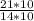
Производная по определению - предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует.
Δy = f(x+Δx) - f(x) = √(1+2(x+Δx)) - √(1+2x) = √(1+2x+2Δx) - √(1+2x)
Преобразуем выражение, домножив числитель и знаменатель на сопряженное выражение:
(√(1+2x+2Δx) - √(1+2x))(√(1+2x+2Δx) + √(1+2x))/(√(1+2x+2Δx) + √(1+2x)) = (1+2x+2Δx - 1 -2x)/(√(1+2x+2Δx) + √(1+2x))= (2Δx)/(√(1+2x+2Δx) + √(1+2x))
Δy/Δx = 2/(√(1+2x+2Δx) + √(1+2x))
limΔx->0 (2/(√(1+2x+2Δx) + √(1+2x)) = 2/(√(1+2x) + √(1+2x)) = 2/(2√(1+2x) = 1/√(1+2x)
ответ: y' = 1/√(1+2x)
Вычтем из первого уравнения системы второе:
Если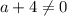 , то в силу того, что произведение равно нолю,
, то в силу того, что произведение равно нолю, 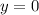 . И, подставляя это, например, во второе уравнение, имеем:
. И, подставляя это, например, во второе уравнение, имеем:
Значит, чтобы решений было бесконечно много, нужно чтобы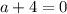 или же
или же 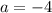 . При этом значении
. При этом значении  переменная
переменная 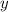 может быть любым числом. И каждому значению переменной соответствует свое значение переменной
может быть любым числом. И каждому значению переменной соответствует свое значение переменной  .
.
Действительно, в этом случае первое и второе уравнение системы будут совпадать с точностью до умножения на два:
Задача решена!
ответ: при a = - 4 .