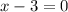и 
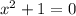
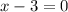равносильно уравнению 
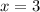, множеством решений которого есть единственное число, а именно: 
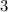, при подстановке в уравнение этого числа уравнение превращается в верное числовое тождество, а именно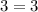 
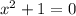равносильно уравнению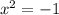 
из множества действительных чисел выполняется следующее неравенство: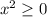 
.
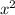не может равняться отрицательному числу, и 
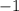в том числе.
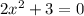и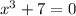 
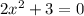не имеет решений на множестве действительных чисел. 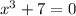равносильно уравнению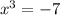 
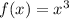монотонно растет (при увеличение аргумента функции, ее значения функции только увеличивается) на множестве своего определения, т.е. на всем множестве действительных чисел
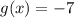- проведенная через точку 
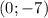параллельно оси ОХ прямая линия. 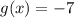и 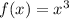пересекаются в одной точке, и эта точка пересечения графиков отвечает единственному действительному решению уравнения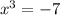 
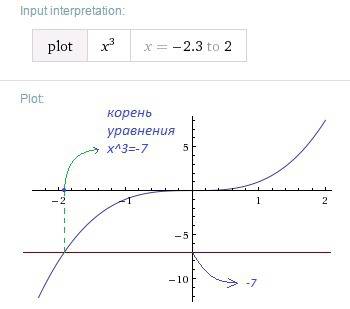
Прицепила файл с таблицей и графиками
Не знаю. как подробней. Это квадратичные функции, положительная и отрицательная. Они симметричны относительно оси 0х. Если старший коэффициент положительный, то ветви параболы направлены вверх, а если старший коэффициет отрицательный, то ветви направлены вниз. В данных функциях нет коэффициента, но можно обозначить его буквой а. Тогда в первой будет y=ax^2, во второй -ax^2. Посмотрите внимательно в приложенной таблице, как значение у меняется в зависимости от а и -а. Например, при x=0.5, y=0.25, y=-0.25; при x=-1, y=1, y=-1, ghb x=-2, y=4, y=-4. Т.е - меняется только знак - при положительном коэффициенте у - положительное число, при отрицательном коэффициете - у - отрицательное число.