1. Разложим, выделив полные квадраты где возможно и посмотрим, можно ли
Вот и получили сумму квадратов, а квадрат любого действительного числа (именно такие мы рассматриваем) неотрицателен, то данное выражение отрицательные значения принимать не может. ответ: нет.
Здесь ситуация аналогичная и ответ: нет.
2. Решаем уравнения
Вторая скобка содержит в себе квадрат и положительное слагаемое, она всегда положительна, так что нулю может быть равна только первая скобка, откуда искомый корень и нашли. ответ:
Произведение равно нулю, когда хотя бы один из сомножителей равен 0, это совокупность на языке множеств.
В порядке убывания ответ будет такой:
3. Просто раскладываем:
4. Аналогично (если вы не проходили, корни, что вероятнее всего, так как это 7-ой класс, то в 1 примере последнее на пиши, остановись на предпоследнем шаге):
Модуль любого числа a= a при a>=0 и -a когда a<0 пример |7|=7 так как 7>0 |-5|=5 так> как -5<0 модуль всегда число равное или большее 0. Это относится и к выражениям, только надо найти х когда выражение положительное и когда отрицательное. |x-1|=x-1 при x-1>=0 x>=1 и -(x-1)=1-x при x-1<0 x<1
Отметим на числовой прямой точки, дающие при делении на 12 остаток 5, красным карандашом, а точки, дающие при делении на 18 остаток 13-синим. Каково будет наименьшее расстояние между красной и синей точкой?
Очевидно : n₁ =12q₁ + 5 ( отмечены красным карандашом); n₂ =18q₂ + 13 (отмечены синим карандашом ) . Расстояние между этими точками будет: d=| n₁ - n₂ | = |12q₁ + 5 -( 18q₂ + 13) | = | 6(2q₁ -3q₂) - 8 | . Значение выражения (2q₁ -3q₂) должна быть не отрицательной (d ≥0) если : 2q₁ -3q₂ =0 ⇒ d =8 ; --- 2q₁ -3q₂ =1 ⇒ d =2 ; --- 2q₁ -3q₂ =2 ⇒ d =4 ; 2q₁ -3q₂ =3 ⇒ d =10 ; и т.д. расстояние увеличивается. Получается d =dmin=2 , если уравнение 2q₁ -3q₂ =1 будет иметь целочисленное решение и оно имеет. Действительно: 2q₁ -3q₂ =1 ⇔2q₁ =3q₂+1 ⇔q₁ =q₂ +(q₂+1)/2 , замена (q₂+1)/2 =t ∈ Z ⇒ q₂ =2t -1 и q₁ =q₂ +(q₂+1)/2= 2t -1 +t =3t -1. {q₁ =3t - 1 ; q₂ =2t -1 . Соответственно : { n₁ =12q₁ + 5 =36t -7 ; n₂ =18q₂ + 13 =36t -5 ; t ∈Z. Бесконечно множество точек : например: t=-1⇒n₁ = - 43 ; n₂ = - 41 ; t=0 ⇒n₁ = -7 ; n₂ = - 5 ; t=1 ⇒n₁ = 29 ; n₂ = 31
ответ : d min =2 .
* * * между точками n₁ =36t -7 и n₂ =36t -5 ; t ∈Z * * *
1. Разложим, выделив полные квадраты где возможно и посмотрим, можно ли
Вот и получили сумму квадратов, а квадрат любого действительного числа (именно такие мы рассматриваем) неотрицателен, то данное выражение отрицательные значения принимать не может. ответ: нет.
Здесь ситуация аналогичная и ответ: нет.
2. Решаем уравнения
Вторая скобка содержит в себе квадрат и положительное слагаемое, она всегда положительна, так что нулю может быть равна только первая скобка, откуда искомый корень и нашли. ответ: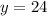
Произведение равно нулю, когда хотя бы один из сомножителей равен 0, это совокупность на языке множеств.
В порядке убывания ответ будет такой:
3. Просто раскладываем:
4. Аналогично (если вы не проходили, корни, что вероятнее всего, так как это 7-ой класс, то в 1 примере последнее на пиши, остановись на предпоследнем шаге):
5. Тут уже даже первое действие дано