Решите на множестве r систему неравенств 14x-9< 3x=14 17x+21> 14x+5 всё это в одной фигурной скобке сначало

👇

Увидеть ответ

Ответ:

khgssfghdwwcnoy

21.05.2023

14x-3x<14+9

17x-14x>5-21

11x<23

3x>-16

x<23/11

x<-16/3

- бесконечности до -5(1/3)

4,8(46 оценок)

Открыть все ответы

Ответ:

pycya2006

21.05.2023

Скорость грузовой машины - 40км/ч.

Выразим скорость грузовой машины через х. Тогда скорость легковой машины - 1,5х (км/ч). Сколько времени ехала грузовая машина? 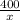$\frac{400}{x}$ часов. А легковая, соответственно, 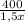$\frac{400}{1,5x}$ часов. Поскольку известно, что выехала она на 2 часа позже, а приехала на 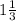$1\frac{1}{3}$ часа раньше, значит, в целом она пробыла в пути на 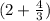$(2 +\frac{4}{3})$ часов меньше.

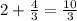$2 +\frac{4}{3}=\frac{10}{3}$ - разница во времени.

Составим уравнение:

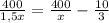$\frac{400}{1,5x}=\frac{400}{x}-\frac{10}{3}$ .

Избавимся от знаменателей, умножив обе части на общий множитель 3х.

Получим: 800 = 1200 - 10х

10х=400

х=40.

А это и есть скорость грузовика

4,8(26 оценок)

Ответ:

Хцжцэ

21.05.2023

y=6x⁵+15x⁴+10x³

1) Область определения: х∈(-∞,+∞) .

2) Множество значений: у∈(-∞,+∞) .

3) Эта кривая не имеет асимптот, так как

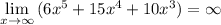$\lim\limits _{x \to \infty}\, (6x^5+15x^4+10x^3)=\infty$ .

Нет точек разрыва.

4) Точка пересечения с осью ОУ (при х=0) одна - это (0,0).

5) Точка пересечения с осью ОХ тоже одна - (0,0), так как

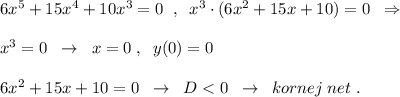
$6x^5+15x^4+10x^3=0\; \; ,\; \; x^3\cdot (6x^2+15x+10)=0\; \; \Rightarrow \\\\x^3=0\; \; \to \; \; x=0\; ,\; \; y(0)=0\\\\6x^2+15x+10=0\; \; \to \; \; D<0\; \; \to \; \; kornej\; net\; .$

6) Интервалы монотонности и точки экстремума функции:

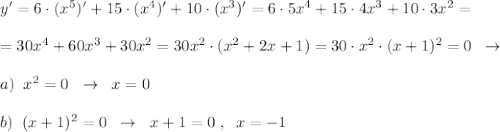
$y'=6\cdot (x^5)'+15\cdot (x^4)'+10\cdot (x^3)'=6\cdot 5x^4+15\cdot 4x^3+10\cdot 3x^2=\\\\=30x^4+60x^3+30x^2=30x^2\cdot (x^2+2x+1)=30\cdot x^2\cdot (x+1)^2=0\; \; \to \\\\a)\; \; x^2=0\; \; \to \; \; x=0\\\\b)\; \; (x+1)^2=0\; \; \to \; \; x+1=0\; ,\; \; x=-1$

Подсчитаем знаки производной y' на полученных интервалах:

$+++[-1\, ]+++[\, 0\, ]+++$

При переходе через точки х=0 и х= -1 производная не меняет знак, значит точки х=0 и х= -1 не являются точками экстремума. А на промежутках, где производная всюду положительна, сама функция возрастает.

Интервалы возрастания функции: x∈(-∞,-1 ]∪[-1,0 ]∪[0,+∞) .

7) Интервалы выпуклости и вогнутости, точки перегиба функции:

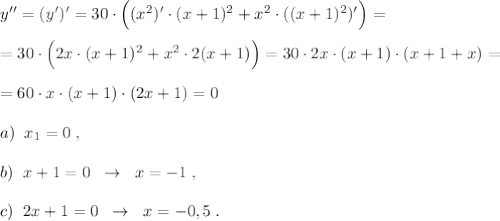
$y''=(y')'=30\cdot \Big ((x^2)'\cdot (x+1)^2+x^2\cdot ((x+1)^2)'\Big )=\\\\=30\cdot \Big (2x\cdot (x+1)^2+x^2\cdot 2(x+1)\Big )=30\cdot 2x\cdot (x+1)\cdot (x+1+x)=\\\\=60\cdot x\cdot (x+1)\cdot (2x+1)=0\\\\a)\; \; x_1=0\; ,\\\\b)\; \; x+1=0\; \; \to \; \; x=-1\; ,\\\\c)\; \; 2x+1=0\; \; \to \; \; x=-0,5\; .$

Определим знаки второй производной y'' на интервалах:

$---[-1\, ]+++[-0,5\, ]---[\, 0\, ]+++$

На промежутках, где y''<0, функция y(x) выпукла, а там, где y''>0, функция вогнута. Точки перегиба - те точки, при переходе через которые у'' меняет знак,это х= -1 , х= -0,5 , х=0 .

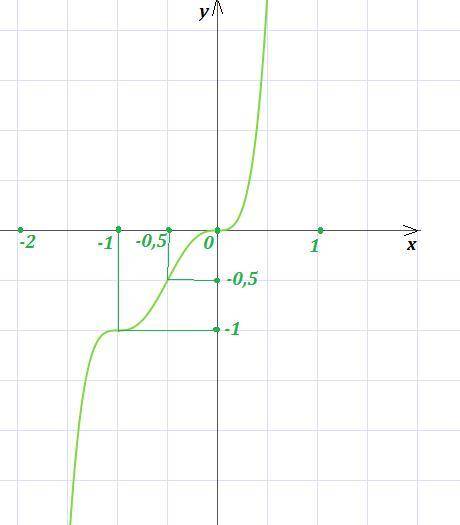
8) Для более точного построения графика найдём координаты некоторых промежуточных точек: (-1,-1) , (-0,5 ; -0,5) .

График на рисунке.