РЕШИТЬ ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ ВЫБРАТЬ КОРНИ
1. x=81
2. x=−81
3. x=
4. x=
Выберите корни уравнения
log5(−2x−62)=0
1. x=7
2. x=−7
3. x=−9
4. x=9
Выберите корни уравнения
(33x−1)−x=0
1. 32
2.
3.
4. −32
Выберите корень уравнения
2x+4=2
1. \frac{2}{3}
2. -\frac{3}{2}
3. -\frac{2}{3}
4. \frac{3}{2}
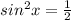
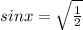ИЛИ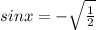 
.
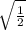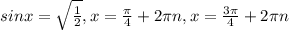
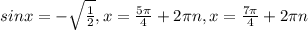
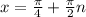, n∈Z (n принадлежит целым числам).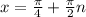
Пусть дана окружность с центром О и в нее вписан треугольник ABC. Соединим центр окружности О с вершинами A и B треугольника, а также опустим высоту ОE на сторону AB с центра окружности. Рассмотрим треугольник OEB, OE перпендикулярна AB, то есть угол OEB – прямой, OB = R (радиусу вписанной окружности) и OE = R/2 (по условию).
Тогда по теореме Пифагора имеем:
BE² = OB² – OE² = R² – (1/4)*R² = (3/4)R²
BE = √((3/4)R²) = R√3 / 2
Так как АО = ОВ и катет ОЕ – общий, то ΔАЕО = ΔВЕО.
Отсюда следует: ЕА = R√3 / 2
Тогда АВ = ВЕ + ВЕ = R√3 / 2 + R√3 / 2 = R√3
Что и требовалось доказать