х∈ (-∞, -2].
Объяснение:
Решить систему неравенств:
-х²+х+6<=0
5-3(x+1)>x
Решим первое неравенство как квадратное уравнение:
-х²+х+6=0/-1
х²-х-6=0
х₁,₂=(1±√1+24)/2
х₁,₂=(1±√25)/2
х₁,₂=(1±5)/2
х₁= -4/2
х₁= -2
х₂=6/2
х₂=3
Смотрим на уравнение. Уравнение параболы.
Начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает уравнение, ветви направлены вниз, парабола пересекает ось Ох при х= -2 и х=3. По графику ясно видно, что у<=0 (как в неравенстве) слева и справа от значений х, то есть, решения неравенства в интервале х∈ (-∞, -2]∪[3, +∞).
Значения х= -2 и х=3 входят в число решений неравенства, скобка квадратная.
Это решение первого неравенства.
Решим второе неравенство.
5-3(x+1)>x
5-3х-3>x
-3x-x> -2
-4x> -2
x< -2/-4 знак меняется
x<0,5
х∈ (-∞, 0,5) - решение второго неравенства.
Неравенство строгое, скобки круглые.
Теперь на числовой оси нужно отметить оба интервала и найти пересечение решений, которое подходит двум неравенствам.
Отмечаем на числовой оси числа -2, 0,5, 3.
Штриховка от -2 до - бесконечности, от 0,5 до - бесконечности, от 3 до + бесконечности.
Пересечение от -2 до - бесконечности.
Решения системы неравенства находятся в интервале х∈ (-∞, -2].
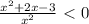
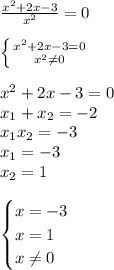
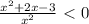є два -2 і -1
ответ: (1;-4)
Объяснение: 3x-y=7, y=3x-7; 2x+3y=-10, 2x=-10-3*(3x-7)
y=3x-7. 2x=-10-9x+21
y=3*1-7 2x+9x=11
y=-4 11x=11
x=1
ответ:(1;-4)