Скорость грузовой машины - 40км/ч.
Выразим скорость грузовой машины через х. Тогда скорость легковой машины - 1,5х (км/ч). Сколько времени ехала грузовая машина?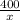 
часов. А легковая, соответственно, 
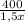часов. Поскольку известно, что выехала она на 2 часа позже, а приехала на 
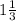часа раньше, значит, в целом она пробыла в пути на 
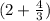часов меньше.
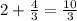- разница во времени.
Составим уравнение:
.
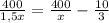Избавимся от знаменателей, умножив обе части на общий множитель 3х.
Получим: 800 = 1200 - 10х
10х=400
х=40.
А это и есть скорость грузовика
ответ:6
Объяснение:1. Заметим, что никакое число, не превосходящее 1015, не может иметь высоту 4. Действительно, наименьшее число высоты 4 — это
2222=216, при этом это число больше 1015.
2. Между тем числа высоты 3, не превосходящие 1015, существуют. Например, 16=222 имеет высоту 3. Таким образом, задача свелась к подсчёту количества чисел высоты 3, не превосходящих 1015.
3. Заметим, что
29≤1015≤210,
36≤1015≤37,
44≤1015≤45,
54≤1015≤55,
63≤1015≤64.
4. Найдём количество чисел высоты 3, не превосходящих 1015. Это то же самое, что найти количество решений неравенства:
x1x2x3≤1015, xi≥2.
Если x1=2, то x2x3≤9, отсюда x2=x3=2, или x2=2, x3=3, или x2=3, x3=2. Отсюда получаем 3 решения.
Далее, если x1=3,4,5, получаем, что x2=x3=2, что даёт ещё три решения.
Наконец, при x1≥6 получаем, что x2x3≤3. Но так как xi≥2, то таких x2, x3 не существует.
5. Таким образом, получаем 3+3=6 чисел максимальной высоты, не превосходящих 1015.