y = f(x)
Сначала осознаем как должен выглядеть график (рис. 1):
Рисуем прямые x = -5 и x = 6, график не должен выходить за эти прямые (обозначили область определения).Рисуем прямые y = -4 и y = 3, график не должен выходить за эти прямые (обозначили множество значений).На оси Ox отмечаем интервал (1;4), график функции должен проходить через ось Ox в этом интервале (обозначили промежуток нулевого значения).Теперь построим график функции (рис. 2):
Для простоты построим график ломанной (она непрерывна и просто изображается).
Функция убывает на всей области определения, поэтому для самого меньшего х из области определения , должно быть самое наибольшее y из множества значений (потом это значение уже не реализуется т.к. функция убывает, тогда множество значений будет другим). Итог: вершина ломанной в точке (-5;3).Пусть следующая вершина в точке (0;2).Ноль функции, он же пусть будет и вершиной ломанной, в точке (3;0) т.к. 3 ∈ (1;4).Последняя вершина в точке (6;-4), y= -4 для нужного множества значений.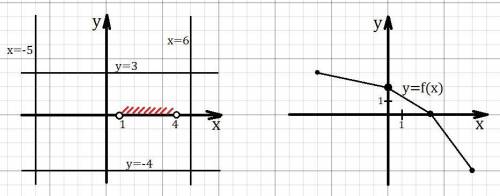
хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз хз