ответ: 2 км/час.
Объяснение:
Дано. Скорость катера 20км/ч.
Он км против течения
22км по течению реки,
затратив на весь путь 3 часа.
Найдите скорость течения реки.
Решение.
Скорость течения реки обозначим через х км/час
Тогда скорость по течению будет 20+х км/час
скорость против течения --- 20-х км/час.
Время против течения составляет 36/(20-х);
Время по течению --- 22/(20+х);
Общее время равно 3 часа.
36/(20-х)+22/(20+х)=3;
36(20+х)+22(20-х)=3(20+х)(20-х);
720+36х+440-22х=1200-3х²;
3х²+36х-22х+720+440-1200=0;
3х²+14х-40=0;
а=3; b=14; c=-40
D=676>0 - 2 корня.
х1=2; х2= -6,66 - не соответствует условию
х=2 км/час - скорость течения реки.
Проверим:
36/18 + 22/ 22= 2+1=3 часа. Всё верно!
а)f'(x) =6x-6x²=6x(1-x). Критические точки из уравнения 6х(1-х)=0.
х=0 и х=1.
Обе точки на данном интервале. -1___-___0___+___1-__2 .
Знаки можно не определять, а обойтись только сравнением значений.
у(-1)=3*(-1)²-2*(-1)³ = 5.
у(0)=0
у(1)=1
у(2)=-4. Сравниваем. Наибольшее равно 5, наименьшее равно -4.
Во втором полная аналогия, f'(x)=3x²-12x=3x(x-4).
Критические точки 0 и 4, на интервале только 0.
Вычисляем у(-2)=-32, у(0)=1, у(1)=-4. Наибольшее равно 1, наименьшее -32.
в)f'(x)=5cosx-2sin2x.
Критические точки из уравнения 5cosx-4sinx*cosx=0
cosx=0 или sinx=5/4. x=π/2, а во втором корней нет. Сравниваем
у(0)=0+1=1, у(π/2)=5-1=4 и у(π) 0+1=1. Наибольшее 4, наименьшее 1.
По формуле n-го члена арифметической прогрессии: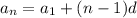 , найдем разность прогрессии
, найдем разность прогрессии
Да, число 30,4 является членом арифметической прогрессии