{3/4; 1}
Объяснение:
Находим нули функции y = 4·x²-7·x+3:
y = 0 ⇔ 4·x²-7·x+3=0.
то есть решаем последнее квадратное уравнение.
Найдем дискриминант квадратного уравнения 4·x²-7·x+3=0, сравнивая общим видом a·x²+b·x+c=0 квадратного уравнения:
D = b²-4ac = (-7)²-4·4·3 = 49-48 = 1 = 1²,
x₁ = (-b - sqrt(D)) / (2·a) = (7 - 1) / (2·4) = 6/8 = 3/4,
х₂ = (-b + sqrt(D)) / (2·a) = (7 + 1) / (2·4) = 8/8 = 1.
0,75; 1.
Объяснение:
Нули функции - это значения аргумента, при которых функция равна нулю.
Для того чтобы найти нули функции, надо решить уравнение:
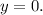
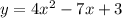
Тогда решим квадратное уравнение
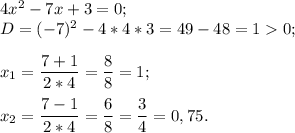
В решении.
Объяснение:
Какова область определения функции у = 5/√8х - 4х²?
Область определения - это значения х, при которых функция существует, проекция графика на ось Ох.
Обозначение D(f) или D(у).
Дана функция у = 5/√8х - 4х²
Так как в данном выражении в знаменателе корень, подкоренное выражение должно быть больше либо равно нулю.
Функция определена, если знаменатель не равен нулю.
Поэтому найти значения х через неравенство:
8х - 4х² > 0
Приравнять к нулю и решить как квадратное уравнение:
8х - 4х² = 0 (неполное квадратное уравнение)
4х(2 - х) = 0
Приравнять множители поочерёдно к нулю:
4х = 0
х₁ = 0;
2 - х = 0
-х = -2
х₂ = 2.
При х=0 и х=2 подкоренное выражение равно нулю, что не допустимо.
Поэтому х может быть любым, кроме х=0 и х=2.
Область определения D(у) = х∈R : х≠0; х≠2.
1
3/4
Объяснение:
для этого необходимо решить уравнение
4х²-7х+3 = 0
найдем дискриминант
D = b²-4ac = (-7)²-4*4*3 = 49-48 = 1
D>0, следовательно, у этого уравнения два корня
х1 = -b + sqrt(D) / 2a = 7 + 1 / 8 = 1
х2 = -b - sqrt(D) / 2a = 7 - 1 / 8 = 6/8 = 3/4