Сначала найдём значения параметра k. Приравняем оба графика, поскольку они пересекаются, а затем уже наложим дополнительные условия.
kx = -x² - 1
x² + kx + 1 = 0
Графики будут иметь одну общую точку тогда и только тогда, когда данное квадратное уравнение будет иметь 1 корень. Найдём те k, при которых данное квадратное уравнение имеет 1 корень. Если квадратное уравнение имеет 1 корень, то его дискриминант строго равен 0.
D = b² - 4ac = k² - 4
D = 0 k² - 4 = 0
k² = 4
k1 = 2; k2 = -2
Значит, при k = 2 и при k = -2 оба графика буцдут иметь ровно одну общую точку.
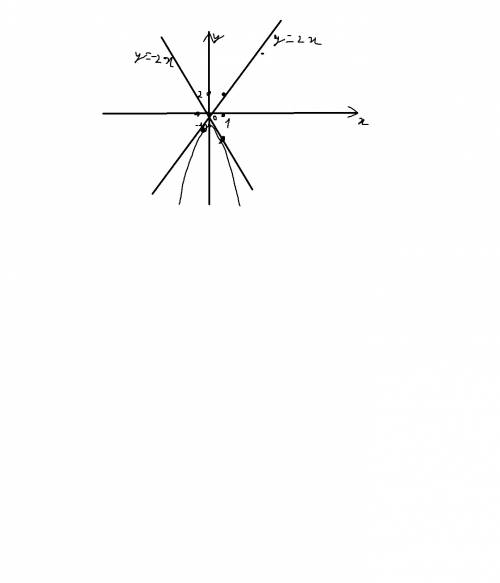
Теперь построим такие прямые. Надо построить y = -x² - 1 и прямые y = 2x, y = -2x. Скажу просто на всякий случай, что обе прямые будут симметричны относительно оси ox. Сейчас пришлю рисунок с построением(надеюсь, вы понимаете, как строятся эти прямые). Построение лишь приближённое и грубое, но видно, что обе прямые касаются параболы в какой-то точке, то есть фактически имеет с ней одну единственную точку.
пусть собственная скорость катера будет = х км/ч, а скорость течения реки = у км/ч
значит скорость катера по течению реки составит: (х+у) км/ч, а против течения (х-у) км/ч
за 1 час по течению катер проплыл 18 км => 1*(x+y) = 18
против течению катер плыл такое же рассстояние, но за 1,5 часа (2,5 - 1) ,т.е. 1,5(х-у) = 18
объединим полученные уравнение в систему и решим их
{ 1*(x+y) = 18
{1,5(х-у) = 18
***
{х = 18 - у
{ 27 - 3у = 18
***
{ у = 3
{ х = 15
скорость течения реки 3 км/ч, а собственная скорость катера 15 км/ч