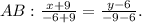
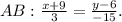
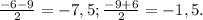
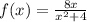. Важно заметить, что по х ты берёшь числа, а вот по у не берёшь, а получаешь. Всё, что может помешать данной функции быть определённой - это знаменатель. На ноль делить нельзя. Таким образом, функция не определена, когда 
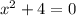, но таких вещественных 
не бывает, поэтому 
.
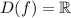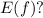Например, можно решать эту задачу, используя производные. Я же приведу здесь другое решение.
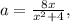где x - неизвестная. Таким образом, мы найдём прообраз точки а, если он есть. Если решение есть, то точка 
входит в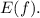 
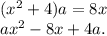
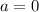Преобразуем:
имеем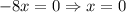 
- точка подходит. Иначе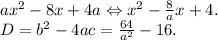
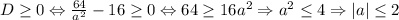
![E(f) = [-2; 2]](/tpl/images/0579/7455/5b169.png)
если cos(п-a) или сos(2п- а), то косинус не меняется на синус. Если же сos(п/2) или cos(3п/2), то косинус поменяется на синус, то же самое с синусом. cos(п-а)+Sin(п/2+а)= -сosa-сosa=-2cosa.