Пусть первый рабочий может убрать помещение за х часов, тогда второй - за (х-3) часов.
Принимаем всю работу, которую нужно выполнить, за 1. Тогда производительность труда (т.е., объём работы за 1 час) первого рабочего равна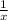 
, а второго - 
.
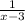Всю работу оба рабочие, работая вместе, выполняют за 2 часа. Первый за это время уберет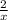 
часть помещения, а второй - 
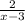. Составляем уравнение:
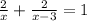x≠0, x≠3
2(х-3)+2х=х(х-3)
2х-6+2х-х²+3х=0
х²-7х+6=0
По теореме Виета: х₁=1 - не подходит, т.к. второй тогда выполнит работу за отрицательное количество часов.
х₂=6
ответ. 6 часов.
1. x,y.z - искомые числа. Тогда составим систему 3-х уравнений исходя из условий задачи.
z = 2x+3
y = x+2
y+z = x^2 +1
Сложим первые два и приравняем к третьему:
3х+5 = x^2 +1. x^2 - 3x - 4 = 0
x1 = -1 не подходит по смыслу задачи (иначе все числа бы на х делились без остатка)
х2 = 4 Тогда у = х+2 = 6, z = 2x+3 = 11.
Сумма этих чисел: х+у+z = 21
ответ: 21.
2. Заданная функция монотонно убывающая с обрывом в точке х = 4.
На отрезке{5; 6] ее оласть значений: [ f(6); f(5)].
f(6) = 5,5. f(5) = 9.
ответ: [ 5,5; 9].
3. Для обратно пропорциональной зависимости:
y = k/x, и никак по другому(!). Во сколько раз увеличивается аргумент, во столько же раз уменьшается функция, и - наоборот.
То есть обязательно коэффициенты a и b = 0 ! К сожалению ни в одном из вариантов ответа нет : a=b=0 !