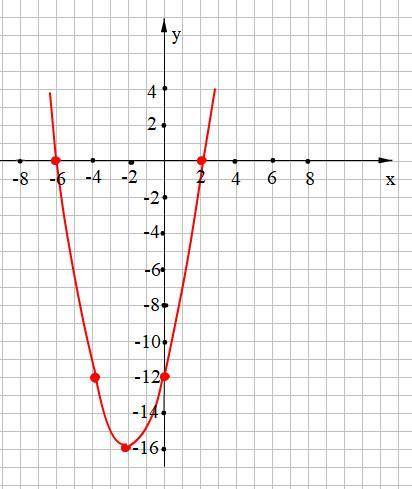
Функция у = х² + 4х - 12
График функции - квадратная парабола веточками вверх
Найдём характерные точки этой параболы.
1) Точка пересечения с осью Оу: х = 0; у = -12;
2) точки пересечения с осью Ох: у = 0
х² + 4х - 12 = 0
D = 4² - 4 · (-12) = 64
√D = 8
x₁ = (-4 - 8)/2 = -6
x₂ = (-4 + 8) = 2
Получили две точки (-6; 0) и (2; 0)
3) найдём координаты вершины С параболы С(m; n)
m = - b/2a = -4/2 = -2
n = y(-2) = (-2)² + 4 · (-2) - 12 = -16
C(-2; -16)
По найденным точкам строим параболу (смотри прикреплённый рисунок).
По графику находим
а) у > 0 при х ∈ (-∞; -6)∪(2; +∞); y < 0 при х ∈ (-6; 2)
б) у↑ при х ∈ (-2; +∞); у↓ при х ∈ (-∞; -2)
в) у наим = у(-2) = -16; наибольшего значения не существует.
Скорость второго рабочего v₂ деталей в минуту
Пусть в партии S деталей.
Тогда
(S-15)/v₁=S/(2v₂) - время, за которое 2-й сделал половину партии.
S/v₁=(S-8)/v₂ - время, за которое 1-ый сделал всю партию.
Если х - искомое количество деталей, то
(S-x)/v₂=S/(2v₁) - время, за которое 1-ый сделал половину партии.
Отсюда x=S(1-v₂/(2v₁)).
Из 1-го и 2-го уравнений получим
v₁/v₂=S/(S-8) и v₁/v₂=2(S-15)/S, т.е.
S^2=2(S-8)(S-15).
Решаем это квадратное уравнение, получаем корни 6 и 40.
6 не подходит, т.к. количество деталей больше 6.
Значит S=40, откуда v₁/v₂=40/(40-8)=5/4, откуда x=40*(1-4/10)=24.
ответ: 24 детали.