Денис загадал четыре различных натуральных числа. Он утверждает, что произведение наименьшего и наибольшего чисел равно 40
произведение двух оставшихся чисел равно 22
Чему равна сумма всех четырёх чисел?
Вдоль дороги стоят дома Андрея, Бори, Васи и Гены (именно в таком порядке). Расстояние между домами Андрея и Гены равно 2550 метрам. Однажды ребята решили устроить забег на 1 К м. Они поставили старт на полпути от дома Андрея до дома Васи. При этом финиш оказался ровно на полпути от дома Бори до дома Гены. Чему равно расстояние от дома Бори до дома Васи? ответ укажите в метрах.
Числа 1 3 4 6 8 11 расставили в клетки фигуры, изображённой на рисунке, так, чтобы суммы чисел во всех столбцах (включая столбец из одной клетки) были равны. Какое число может стоять в самой верхней клетке? Укажите все возможные варианты.
1
3
4
6
8
11
В понедельник 4 человека из класса получили пятёрки по математике, во вторник пятёрки получили 10 человек, в среду — 5 человек, в четверг — 3 человека, в пятницу — 11 человек. Никто из учеников не получал пятёрки два дня подряд. Какое наименьшее количество учеников могло учиться в классе?
На собрании совета племени по очереди выступали 72 человека. Каждый из них сказал только одну фразу. Первые трое выступавших сказали одно и то же: «Я всегда говорю правду». Следующие 69 выступавших тоже сказали одинаковые фразы: «Среди предыдущих трёх выступавших правду сказали ровно два человека». Какое наибольшее количество выступавших могло сказать правду?
В кабинете есть несколько одиночных парт (за каждой партой может сидеть не более одного человека; других парт в кабинете нет). Во время перемены четверть учащихся вышли в коридор, а в кабинете осталось количество людей, равное 4/7 от общего числа парт. Сколько парт в аудитории, если их не более 30?
Таня и Вера играют в игру. У Тани есть карточки с числами от 1 до 30. Она расставляет их в некотором порядке по кругу. Для каждых двух соседних чисел Вера считает их разность, вычитая из большего числа меньшее, и выписывает получившиеся 30 чисел себе в блокнот. После этого Вера отдает Тане количество конфет, равное наименьшему числу из выписанных в блокнот. Таня выкладывает карточки так, чтобы получить как можно больше конфет. Какое наибольшее количество конфет она может получить
 часа.
часа.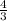 часа - 3 кг сплава
часа - 3 кг сплава кг сплава
кг сплава часа.
часа. часа - 3 кг сплава
часа - 3 кг сплава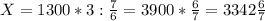 кг сплава
кг сплава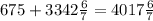 кг сплава
кг сплава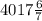 кг сплава.
кг сплава.
1. 22 = 2·11
2 и 11 - два числа.
Произведение наименьшего и наибольшего равно 40. Значит 1 - наименьшее, 40 - наибольшее.
2+11+1+40 = 54 - сумма всех чисел.
ответ: 54.
2. Расстояние между домами Андрея и Гены можно разделить на 3 отрезка:
1) от дома Андрея до места старта (половина расстояния АВ);
2) от места старта до места финиша (1000 м);
3) от места финиша до дома Гены (половина расстояния БГ).
Получается
0,5·АВ+1000+0,5·БГ = 2550
0,5·АВ+0,5БГ = 2550-1000
0,5·(АВ+БГ) = 1550
АВ+БГ = 3100
В последней сумме расстояние БВ посчитано дважды. То есть
БВ = 3100-2550 = 550 м.
ответ: 550 метров.
3. Нет рисунка.
4. 4+10 = 14 - в понедельник и вторник
10+5 = 15 - во вторник и среду
5+3 = 8 - в среду и четверг
3+11 = 14 - в четверг и пятницу.
Наименьшее учеников в классе составляет 15.
5. Если из первых троих соврал первый, а второй и третий сказали правду, то четвёртый тоже сказал правду, пятый соврал, шестой, седьмой и восьмой сказали правду, девятый соврал и т.д. То есть наибольшее количество выступавших скажут правду, если правду будет говорить трое из 4 выступивших
72:4·3 = 54
ответ: 54.
6. Пусть в аудитории x парт, при этом x кратно 7 не превышает 30, то есть парт может быть 7, 14, 21 или 28.
4/7x учащихся осталось в кабинете, что составляет 3/4 от всего количества учащихся, то есть
Очевидно, что x должен быть кратен 21, то есть x = 21.
ответ: 21.
7. Если Таня расставит карточки так:
1; 16; 2; 17; 3; 18 и так далее, то разность двух соседних чисел будет составлять 14 или 15 (кроме единицы и числа слева от неё - там будет 30 и разность 29).
То есть наибольшее конфет, которое может получить Таня, равно 14.
ответ: 14.