Объяснение:
y=5ˣ.
Это показательная функция.
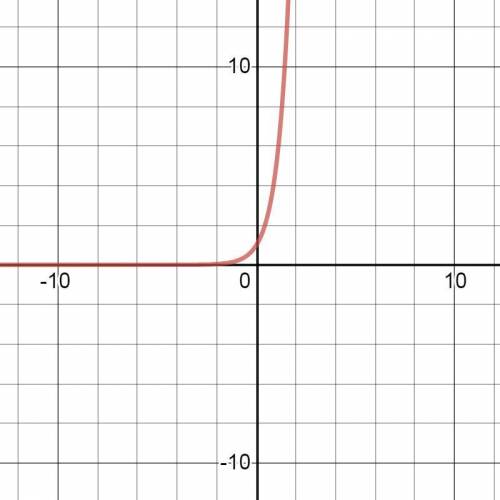
График этой функции показан на рис. 1.
Показательная функция y=5ˣ является строго монотонно возрастающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
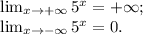
у=0,3ˣ
Это показательная функция.
График этой функции показан на рис. 2.
Показательная функция у=0,3ˣ является строго монотонно убывающей.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у∈(0;+∞).
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
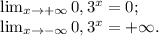
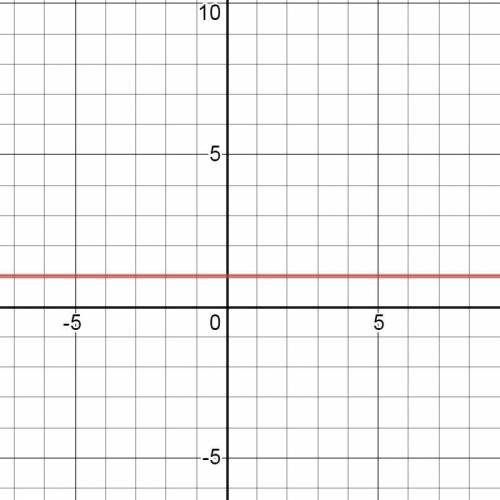
у=1ˣ.
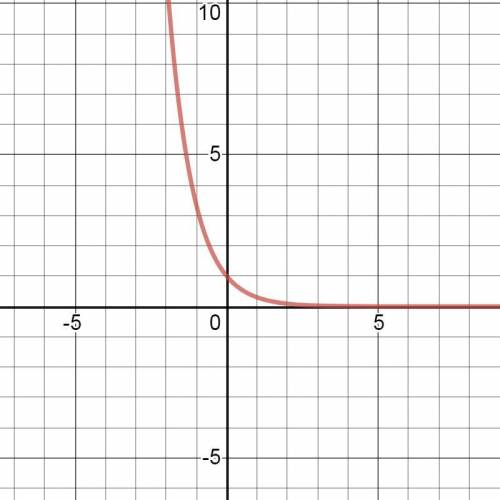
График этой функции показан на рис. 3.
Единица в любой степени равена единице. ⇒
Получаем функцию у=1.
Графиком этой функции является график функции у=0 (ось ОХ),
смещённый вверх по оси ОУ на одну единицу.
Область определения функции: х∈(-∞;+∞).
Область значений функции: у=1.
Точки пересечения с осью ОХ: нет.
Точки пересечения с осью ОУ: х=0 (0;1).
у=2х-7 искомое уравнение.
Объяснение:
Составьте уравнение вида y = kx+ b, график которого проходит через данные точки C (-3;-13) и D (1;-5)
Формула, при которой можно построить уравнение прямой по двум точкам:
(х-х₁)/(х₂-х₁)=(у-у₁)/(у₂-у₁)
C (-3;-13) и D (1;-5)
х₁= -3 у₁= -13
х₂=1 у₂= -5
Подставляем данные в формулу:
(х-(-3)/(1-(-3)=(у-(-13)/(-5)-(-13)
(х+3)/4=(у+13)/8 перемножаем крест-накрест, как в пропорции:
8(х+3)=4(у+13)
8х+24=4у+52
-4у= -8х+52-24
-4у= -8х+28
4у=8х-28/4
у=2х-7 искомое уравнение.