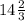Для решения данной задачи нам нужно найти приближенное значение выражения cd, где c = -0.1130786... и d = 2.4123109..., при предварительном округлении значений c и d до десятых.
Шаг 1: Округление значений c и d до десятых.
Значение c округляем до десятых: c ≈ -0.1
Значение d округляем до десятых: d ≈ 2.4
Шаг 2: Вычисление приближенного значения выражения cd.
cd ≈ (-0.1) * (2.4) = -0.24
Таким образом, приближенное значение выражения cd, при предварительном округлении значений c и d до десятых, равно -0.24.
Обоснование:
Округление чисел c и d до десятых происходит в соответствии с правилами округления. Затем, округленные значения c и d подставляются в выражение cd и производится умножение. Получившийся результат, -0.24, является приближенным значением выражения cd.
Важно помнить, что округление в данном случае применяется с целью получения приближенного значения, и окончательный ответ может отличаться от точного результата.
#1. |2x-3|=3-2x, если х<3/2; |2x-3|=2x-3, если х≥3/2;
|x-2|=2-x, если х<2; |x-2|=-2x, если х≥2;
|x-6|=6-x, если х<6; |x-6|=x-6, если х≥6.
Получаем три случая:
1) на множестве (-∞;3/2)U[2;6) получаем неравенство
(2х-3)(х-2)≥(6-х)+2
2х²-3х-4х+6-6+х-2≥0
2х²-6х-2≥0
х²-3х-1≥0
D=9+4=13
C учётом (-∞;3/2)U[2;6) получим![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
2) на интервале 1,5≤х<2 получим неравенство
(2х-3)(2-х)≥(6-х)+2
4х-6-2х²+3х-6+х-2≥0
-2х²+8х-14≥0
х²-4х+7≤0
D=16-28<0
решений нет
3) на интервале х≥6 получим неравенство
(2х-3)(х-2)≥(х-6)+2
2х²-3х-4х+6+6-х-2≥0
2х²-8х+10≥0
х²-4х+5≥0
D=16-20<0
решений нет
ответ:![x \in (-\infty; \frac{3-\sqrt{13}}{2}]](/tpl/images/0172/7524/fc8b3.png)
#2. Пусть ∆АВС-прямоугольный треугольник с гипотенузой АВ, катетами АС и ВС.
По условию ВС+АВ=11, tg В = 3/4.
По определению тангенса острого угла прямоугольного треугольника
tg B=AC/BC=3/4 => 3BC=4AC =>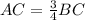
По теореме Пифагора АВ² = АС² + ВС²
Пусть ВС=х, тогда АВ=11-х, АС=3х/4
ответ: