У ванні є два крана. Через перший кран вода наливається у ванну, а через другий — витікає з ванни.
Якщо відкрити обидва крана, то повна ванна випорожниться за 36 хвилин. Скільки хвилин буде наповнюватися ванна, якщо буде відкритий тільки перший кран, і відомо, що через другий кран повна ванна випорожниться на 3 хвилин(-и) швидше, ніж перший кран наповнить порожню ванну.
За скільки хвилин другий кран випорожнить повну ванну?
Перший кран наповнить порожню ванну за
хвилин.
Другий кран випорожнить повну ванну за
хвилин.
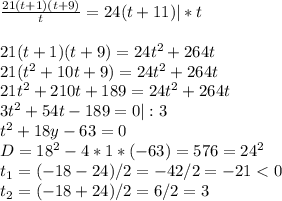
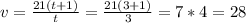(км/ч)
Пусть скорость третьего велосипедиста равна v км/ч,
а t ч - время, за которое он догнал второго велосипедиста.
До встречи третий и второй велосипедисты проехали одно и то же расстояние.
По условию задачи, второй ехал на 1 час больше, чем третий.
Тогда t+1 ч - время второго
Получаем:
Скорость (км/ч) Время (ч) Расстояние (км)
третий v t v*t
второй 21 t+1 21*(t+1)
Составляем первое уравнение: vt=21(t+1)
До встречи первый и третий проехали одинаковое расстояние, третий догнал первого через t+9 часов,
а первый на тот момент уже был в пути t+2+9=t+11 часов, т.к. выехал на 2 часа раньше третьего.
Получаем:
Скорость (км/ч) Время (ч) Расстояние (км)
третий v t+9 v*(t+9)
второй 24 t+11 24*(t+11)
Составляем второе уравнение: v(t+9)=24(t+11)
Решаем систему уравнений:
{ vt=21(t+1) => v=21(t+1)/t (подставим во второе уравнение)
{ v(t+9)=24(t+11)
Итак, t=3 часа
Находим скорость третьего велосипедиста:
ответ: 28 км/ч