Подайте число 60 у вигляді суми двох додатніх чисел, щоб їх добуток був найменшим. отправить номер 60 в виде суммы их двух положительных чисел, так что бы их продукт являлся самым маленьким

👇

Увидеть ответ

Ответ:

банан0008

04.05.2022

ответ: 60 = 30 + 30.

Объяснение:

Нехай 2 додатні числа будуть х і у. Тоді їх сума x+y = 60 ⇒ y=60-x

Розглянемо функцію: f(x) = xy = x * (60 - x) = 60x - x²

Графіком квадратичної функції є парабола, вітки якої напрямлені вниз, звідси точка вершини параболи досягає мінімуму

x = -b/2a = 60/2 = 30

y = 60 - 30 = 30

Отже, 60 = 30 + 30.

4,4(77 оценок)

Открыть все ответы

Ответ:

Yanalime2006

04.05.2022

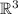Пусть $\varepsilon$ - канонический базис в $\mathbb{R}^{3}$ .

Тогда матрицу перехода 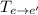$T_{e \rightarrow e'}$ можно найти следующим образом:

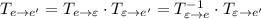
$T_{e \rightarrow e'} = T_{e \rightarrow \varepsilon} \cdot T_{\varepsilon \rightarrow e'} = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

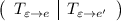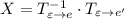
Если записать блочную матрицу $\left(\begin{array}{c|c}T_{\varepsilon \rightarrow e}&T_{\varepsilon \rightarrow e'}\end{array}\right)$ и привести путем элементарных преобразований к виду $\left(\begin{array}{c|c}E&X\end{array}\right)$ , то $X = T_{\varepsilon \rightarrow e}^{-1} \cdot T_{\varepsilon \rightarrow e'}$

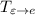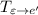Матрицу $T_{\varepsilon \rightarrow e}$ легко получить: достаточно записать в столбцы координаты векторов базиса . Аналогично с матрицей $T_{\varepsilon \rightarrow e'}$ .

В итоге необходимо получить вид $\left(\begin{array}{c|c}E&X\end{array}\right)$ следующей матрицы:

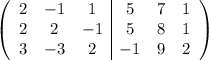
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\2&2&-1&5&8&1\\3&-3&2&-1&9&2\end{array}\right)$

Вычтем первую строку из второй и третьей:

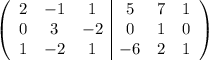
$\left(\begin{array}{ccc|ccc}2&-1&1&5&7&1\\0&3&-2&0&1&0\\1&-2&1&-6&2&1\end{array}\right)$

Вычтем из первой строки 2 третьих и поменяем их местами:

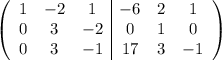
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&3&-1&17&3&-1\end{array}\right)$

Вычтем из третьей строки вторую:

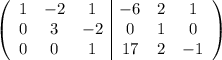
$\left(\begin{array}{ccc|ccc}1&-2&1&-6&2&1\\0&3&-2&0&1&0\\0&0&1&17&2&-1\end{array}\right)$

Прибавим ко второй строке 2 третьих и вычтем из первой третью:

$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&3&0&34&5&-2\\0&0&1&17&2&-1\end{array}\right)$

Делим вторую строку на 3:

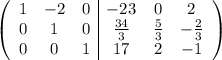
$\left(\begin{array}{ccc|ccc}1&-2&0&-23&0&2\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

Прибавляем в первой строке 2 вторых:

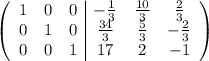
$\left(\begin{array}{ccc|ccc}1&0&0&{-\frac{1}{3}}&\frac{10}{3}&\frac{2}{3}\\0&1&0&\frac{34}{3} &\frac{5}{3}&{-\frac{2}{3}}\\0&0&1&17&2&-1\end{array}\right)$

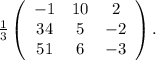
$\frac{1}{3}\left(\begin{array}{ccc}-1&10&2\\34&5&-2\\51&6&-3\end{array}\right).$

4,5(37 оценок)

Ответ:

mytaevafati

04.05.2022

F - первообразная для f, если f = F'. Но так как производная от суммы - это сумма производных, и производная от числа равна нулю, то можно написать f = F' = (F+C)', где С - любое число.

То есть первообразная - это не какая-то одна функция, это класс функций. Для всех разных чисел С - будет разная первообразная F + C, и производная от каждой из них равна f.

У вас в задаче табличные вещи, поэтому гляньте в табличке первообразных.

В общем, первообразная будет

F(х) = 4x + sin(x) + C

Надо, что б если подставить вместо икса П/6, F получилась равной П.

sin(П\6) = 1/2, так как это синус 30 градусов

Получается равенство

П = 4*П\6 + 1\2 + С

6П = 4П+3 + 6С

С = (2П-3)\6

значит F = 4x + sin(x) + (2П-3)/6

4,8(54 оценок)

Это интересно: