При каких значениях параметра a неравенство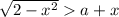 
имеет решения?
ограничения на x: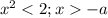 
пусть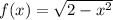 
, тогда:
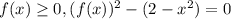
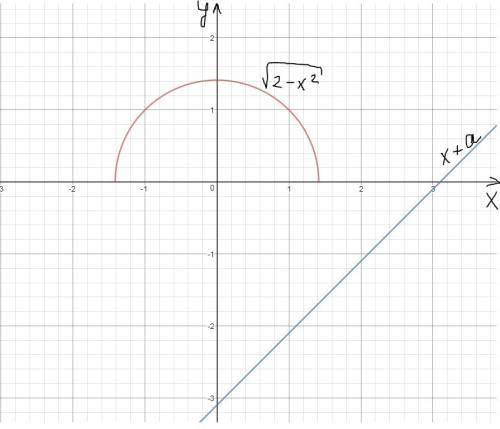
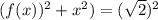- график полуокружности, лежащей выше оси x с центром (0;0) и радиусом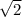 
пусть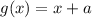 
- график прямой, проходящей через (0; a), т.е. 
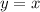смещённый на a вверх-вниз
См. вложения (красным цветом -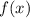 
, синим цветом - 
)
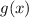график 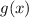должен находиться ниже графика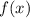
При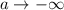 
всегда найдётся такой x, что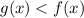 
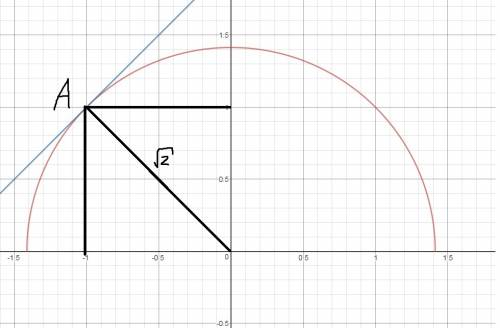
Так будет до касания верхней части окружности (рис.2)
Определим точку касания A:
Её координаты (-1;1), а значит график функции 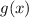имеет вид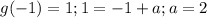 
Следовательно при всех a<2 
имеет решения
ответ: 
Я точно уверен, что здесь нужно использовать производную. Если я правильно понимаю, то производная данной функции будет равна 2x-12+10/x. Чтобы найти нули функции нужно приравнять ее производную к нулю, а затем рассматривать промежутки возрастания и убывания функции. X^2-6X+5. Получаем, что нули производной равны 1 и 5. Расставляем их на прямой. Теперь мы подставляем любое значение из интервала в уравнение производной и смотрим знак. Например, возьмем 10. Производная положительна, а это значит, что функция возрастает. Таким образом функция возрастает от (-беск; 1] и от [5 : +,беск) Нас просят рассмотреть границы 12/13 и 14/13. Как видим, одно число больше 1, другое меньше 1. Причем на одном интервале функция убывает, а на другом возрастает. Не очень понятно какое из значений наименьшее. Таким образом, чтобы найти наименьшее значение функции, нам нужно подставить в функцию вместо x каждую из этих границ и сравнить значения функции.