Если А и В лежат по одну сторону от прямой, то расстояние от середины отрезка до прямой равно полусумме расстояний от концов отрезка до этой прямой. Если лежат по разные стороны от прямой, то полуразности этих расстояний. (12-4)/2 = 4 см.
На промежутке [-2π/3;0] функция cosx возрастает, а у=-2xcosx - убывает. Числа 19 -18/π -постоянные, они не влияют на поведение функции. Наибольшее значение при х = -2π/3. Оно равно 19-2*cos(-2π/3)-18/π = 19-2*(-1/2) -18/π = 20-18/π. Это в том случае, если косинус х.( без скобок).
Данное двойное неравенство равносильно системе двух квадратных неравенств:
Первое неравенство .
.
Заметим, что в левой части скрывается квадрат разности (формула ):
): 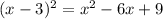 .
.
Неравенство принимает следующий вид: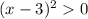 .
.
Так как квадрат числа всегда неотрицательный, то нам не подходит всего лишь один случай: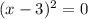 и
и 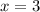 .
.
Значит, первой неравенство эквивалентно тому, что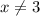 .
.
Второе неравенство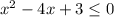 .
.
Вс уравнение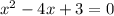 имеет по теореме Виета (утверждающей, что
имеет по теореме Виета (утверждающей, что 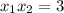 и
и 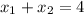 ) корни
) корни 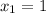 и
и 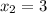 .
.
Из этого следует разложение левой части на множители: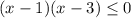 .
.
Метод интервалов подсказывает решение![x \in [ 1; 3 ]](/tpl/images/1227/3957/60bcc.png) .
.
+ + + - - - + + +
_________![[ \; 1 \; ]](/tpl/images/1227/3957/d73a9.png) _________
_________![[ \; 3 \; ]](/tpl/images/1227/3957/abab5.png) _________
_________
\\\\\\\\\\\\\\\\\\\\\
Значит, второе неравенство равносильно тому, что .
.
Имеем значительно более простую систему неравенств:
Вполне понятно, что ее решением является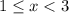 (как пересечения двух промежутков).
(как пересечения двух промежутков).
Или же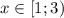 .
.
Задача решена!
ответ: