Объяснение:
Посчитаем:
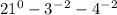
Тут выражение, равное разности степеней чисел 21 , 3 и 4
Свойство степени числа такое:
1. если показатель (цифра сверху) положительное (больше нуля), то пишем обычную степень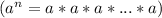 
.
2. если показатель равен нулю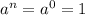 
3. если показатель меньше нуля, то пишем так: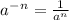 
Рассмотрим на нашем примере и посчитаем:
1) 21 в 0 степени - 1 по второму свойству.
2) 3 в степени -2 равно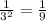 
по 3 свойству.
3) 4 в степени -2 равно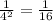 
по 3 свойству.
А затем выполним над ними операции, приведя к общему знаменателю:
144, так как 144 делится и на 16, и на 9 , чтобы было удобнее считать.
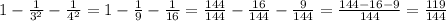
- положительное число, то есть число. которое больше 0. Что и требовалось доказать.
Объяснение:
1. x^2 - 4x - 32 = 0
D = (-4)^2 - 4 * 1 * (-32) = 16 + 128 = 144
x₁ = (4 - √144) / 2 = (4 - 12) / 2 = -4
x₂ = (4 + √144) / 2 = (4 + 12) / 2 = 8
x^2 - 4x - 32 = (x + 4) * (x - 8)
4x^2 - 15x + 9 = 0
D = (-15)^2 - 4 *4 * 9 = 225 - 144 = 81
x₁ = (15 - √81) / (2 * 4) = (15 - 9) / 8 = 0,75
x₂ = (15 + √81) / (2 * 4) = (15 + 9) / 8 = 3
4x^2 - 15x + 9 = 4 * (x - 0,75) * (x - 3) = (4x - 3) * (x - 3)
2. x^4 - 35x^2 - 36 = 0
Пусть t = x^2
t^2 - 35t - 36 = 0
D = (-35)^2 - 4 * 1 * (-36) = 1225 + 144 = 1369
t₁ = (35 - √1369) / 2 = (35 - 37) / 2 = -1
t₂ = (35 + √1369) / 2 = (35 + 37) / 2 = 36
Вернёмся к замене
x^2 = -1
x = ±√-1
x = ± i
x^2 = 36
x = ±6
x + 2 ≠ 0 ⇒ x ≠ -2
Умножим обе части дроби на x+2
x^2 - 7x -18 = 0
x₁ = -2 - не имеет смысла
ответ : 9
3. 4a^2 + a - 3 = 0
D = 1^2 - 4 * 4 * (-3) = 1 + 48 = 49
a₁ = (-1 - √49) / (2 * 4) = (-1 - 7) / 8 = -1
a₂ = (-1 + √49) / (2 * 4) = (-1 + 7) / 8 = 0,75
4a^2 + a - 3 = 4 * (a + 1) * (a - 0,75) = (a + 1) (4a - 3)