Объяснение:
((a+7)\(a-7)-(a-7)\(a+7))\(14\(a^2-7a))
Приведем дроби в скобке к общему знаменателю a^2-49, домножив первую дробь на (a+7), а вторую на (a-7):
((a+7)^2-(a-7)^2)\(a^2-49)
По формуле разности квадратов:
((a+7-a+7)(a+7+a-7))\(a^2-49)
14*2a\a^2-49
28a\a^2-49
Представим деление одной дроби на другую умножением первой на перевернутую вторую:
(28a*(a^2-7a))\(14*(a^-49))
Вынесем в числителе "а" за скобку, а в знаменателе разложим скобку на множители:
(28a^2*(a-7))\(14(a-7)(a+7))
Сократим дробь:
2a^2\(x+7)
1) если а = 1 , то х ∈ R
если а не равнo 1, то 0x=0 =>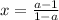
2) если а = -1 , то 0x=0 => х ∈ R
если а ≠ -1, то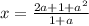
3) ax - 3 = x +3a
ax - x = 3a +3
(a-1)x = 3(a+1)
если а = 1 , то 0x=6 => х ∈ ∅
если а ≠ 1, то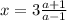
Объяснение:
как то так