1. Простым языком: мода - то число, которое встречается чаще, медиана - это то числа, справа и слева от которого находится равное кол-во чисел.
Моды в данном случае две: 1) 6; 2) 8, т.к. эти числа встречаются в выборке чаще других.
Медиану легко найти, заметив, что всего чисел 9. Т.е. медианой будет число, стоящее на 5 месте в выборке, т.к. оно делит ее на две равные половины: справа от 5 элемента будет 4 числа и слева от него будет 4 числа. На 5 месте стоит число 8 - это и есть медиана.
Среднее значение ищем как среднее арифметическое - складываем все числа и делим на их количество: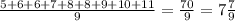 
ОТВЕТ: мода - 6; 8. Медиана - 8. Среднее значение -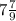 
.
2. Всего карточек - 15. Вероятность будем искать, воспользовавшись классическим определением вероятности: вероятность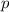 
равна отношению числа 
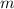благоприятных исходов к общему числу 
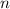исходов: 
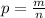. Заметим, что во всех случаях, очевидно, 
.
1) Выбираем из 15 первых натуральных чисел те, что кратны 4: это числа 4, 8 и 12, т.е. таких чисел 3. Т.е.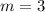 
. Тогда 
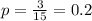(20%)
2) Выбираем из 15 первых натуральных чисел те, которые не кратны ни числу 3, ни числу 5: это числа 1, 2, 4, 7, 8, 11, 13, 14, т.е. таких чисел 8. Т.е.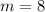 
. Тогда 
.
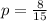ОТВЕТ: 1) 0,2; 2)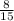 
.
3. Пусть в коробке 
черных шариков. Общее число шаров равно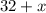 
.
Вероятность того, что выбранный шарик - черный, согласно классическому определению вероятности, равна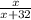 
.
По условию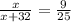 
.
Решаем уравнение; по свойству пропорции:
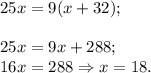
Т.е. всего было 18 черных шаров.
ОТВЕТ: 18.
Монотонная функция -функций, у которой одному значению переменной соответствует только одно значение функции.
Пойдем методом от противного
пусть в точках х и х+с функция принимает одно и то же значение, тогда:
x^3=(x+c)^3
x^3=x^3+3x^2c+3xc^2+c^3
3c *x^2+ 3c^2 *x +c^3=0|:c не равное 0
3x^2+3cx+c^2=0
D=9c^2-4*3c^2=-3c^2<0
Значит не существует такого с, что функция в при нескольких икс принимает одно и то же значение, а значит она монотонна.
Если функция монотонна, то достаточно доказать, что если функция f(х+1) больше функции f(x) -то функция явл возрастающей.
Пусть:
(x+1)^3>x^3
x^3+3x^2+3x+1>x^3
3x^2+3x+1>0
D=9-12=-3<0
Значит уравнение корней не имеет, у параболы ветви вверх, значит она всюду больше 0
Отсюда следует, что:
(x+1)^3>x^3
f(x+1)>f(x)
Значит функция является монотонно возрастающей.