Рассмотрим первое уравнение:
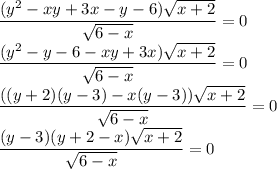
Дробь равна нулю, когда числитель равен нулю (то есть каждый множитель может быть равным нулю), а знаменатель не равен нулю:
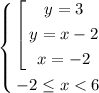
Ограничение на x взялось из-за корней. Теперь достаточно построить каждый график совокупности в заданных пределах.
Второе уравнение представляет собой прямую, смещённую по оси Oy.
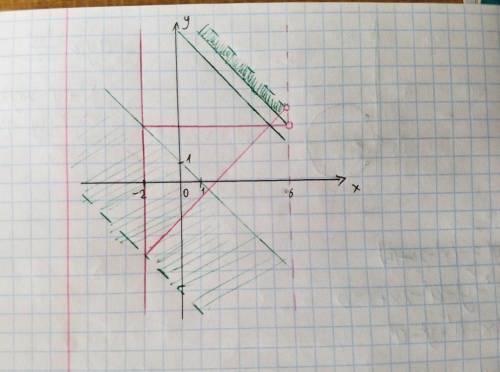
На рисунке красным цветом начерчен график первого уравнения, зелёным — вариации второго. По рисунку видно, что система имеет два решения, если прямая проходит через точку (-2; -4) (не включая такое значение a) и так пробегает до точки (-2; 3), проходит через точку (5; 3), проходит через точку (6; 3) и так пробегает до точки (6; 4) (не включая).
Найдём ключевые значения параметра:
В точке (-2; -4): -2-4-a = 0 ⇔ a = -6;В точке (-2; 3): -2+3-a = 0 ⇔ a = 1;В точке (5; 3): 5+3-a = 0 ⇔ a = 8;В точке (6; 3): 6+3-a = 0 ⇔ a = 9;В точке (6; 4): 6+4-a = 0 ⇔ a = 10.Учитывая рассуждения, получаем ответ.
ответ: ![(-6;1]\cup\{8\}\cup[9;10)](/tpl/images/0537/6712/42e11.png)
а) х=1 у=-7 б) х=7 у=0
Объяснение:
а) 7х-у=14 | +
{
5х+у=-2 |
7х-у+5х+у=14-2
12х=12
х=1
Подставим значение х в 1 уравнение
7×1-у=14
-у=14-7
-у=7
у=-7
б) 3х-у=21 | 4
{
2х+4у=14 |
12х-4у=84
+{
2х+4у=14
12х-4у+2у+4у=84+14
14х=98
х=7
Подставим значение х в 1 уравнение
12×7-4у=84
-4у=0
у=0
Вроде так)