Дана функція:
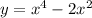
Знайдемо її похідну ( y' = g(x) ):
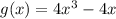
Знайдемо значення похідної в 0 (g(x) = 0):
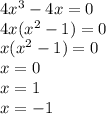
Ми знайшли 3 можливі точки екстремуму: 0, 1, -1. Перевіримо, чи дійсно ці точки є екстремумами функції:
1) Підставимо в похідну точку -2. Значення від'ємне, отже функція спадає;
2) Підставимо в похідну точку -0.5. Значення додатне, отже функція зростає;
3) Підставимо в похідну точку 0.5. Значення від'ємне, отже функція спадає;
4) Підставимо в похідну точку 2. Значення додатне, отже функція зростає.
Отже на проміжку xє(-∞;-1) функція спадає; хє(-1;0) – функція зростає; хє(0;1) – функція спадає; хє(1;+∞) – функція зростає. Отже ці точки дійсно є екстремумами функції.
Відповідь: -1, 0, 1.
ответ: 1)(-∞;+∞)
2)(-∞;1)∪(1;+∞)
3)(-∞;-2)∪(-2;2)∪(2;+∞)
4)(-∞;-3)∪(-3;+∞)
5)(-∞;+∞)
Объяснение:
1) Функция линейная, поэтому данная функция определена при любом х. ответ:(-∞;+∞)
2) Функция дробно-линейная, поэтому областью определения будут все значения х, кроме тех, которые обращают в ноль знаменатель т.е. кроме х=1.ответ:(-∞;1)∪(1;+∞)
3)Функция дробно-линейная, поэтому областью определения будут все значения х, кроме тех, которые обращают в ноль знаменатель т.е х²-4≠0
х²≠4
х≠±2 ответ: (-∞;-2)∪(-2;2)∪(2;+∞)
4) Функция дробно-линейная, поэтому областью определения будут все значения х, кроме тех, которые обращают в ноль знаменатель
3х+9≠0
3х≠-9
х≠-3 ответ:(-∞;-3)∪(-3;+∞)
5)Функция дробно-линейная, поэтому областью определения будут все значения х, кроме тех, которые обращают в ноль знаменатель.Знаменатель х²+3≠0 при любом х. ответ:(-∞;+∞)
вццйвйййййййццццйцйц вот ответ