41-32х≥0;
9-3х≥0
5+х≥0
ОДЗ: х ∈[-5; 41/32]
Перепишем уравнение в виде
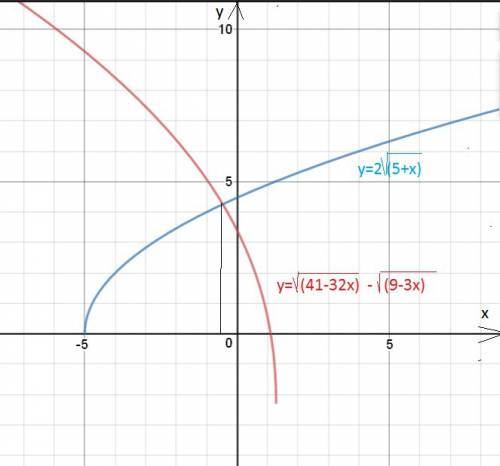
√(41-32x)=2√(5+x)+√(9-3x)
Возводим в квадрат.
41-32х=4(5+х)+4√(5+х)·√(9-3х)+9-3х
4√(5+х)·√(9-3х)=12-33х
Возводим в квадрат при условии 12-33х≥0 ⇒ х ≤12/33.
16(5+х)(9-3х)=144-792х+1089х²;
1137х²-696х-576=0
379х²-232х-192=0
D=(-232)²-4·379·(-192)=53 824+291 072=344 896
x=(232-√344896)/758≈-0,47 или х=(232+√344896)/758≈1,08 - не удовлетворяет условию х ≤12/33, поэтому не является корнем уравнения
У нас уравнение линейное, так? Ну, максимальная степень всех членов равна - один, правильно? Никаких кубов и квадратов. Значит - это линейное уравнение. График у него какой? Правильно - линия, ну, прямая то есть. Тогда надо найти две любые точки на плоскости и провести между ними прямую. Это и будет график функции. Проще всего брать точки пересечения графика с осями координат.
С осью абсцисс (это когда y=0) график пересекается в точке:
0=-3*x+2
x=2/3
Точка один у нас будет (2/3,0) (то есть горизонтальную ось график пересечет в точке 2/3, (две трети это что-то около ноль целых семь десятых) )
С осью ординат (это когда x=0) график пересекается в точке:
y=-3*0+2=2
Точка два у нас будет (0,2)
(то есть вертикальную ось координат график функции пересечет в точке два)
Ну, думаю нарисовала график.
ну, а при y=-4
-4=-3x+2
3x=6
x=2
То есть условие будет выполняться при значении аргумента равном двум.
не определяется,
нет пересеченных с осью x корней