Для решения этой задачи нам потребуется знать, как строится график квадратичной функции. Функция y=x²-2x+3 представляет собой квадратичную функцию вида y=ax²+bx+c, где a, b, и c являются постоянными коэффициентами.
1. Начнем с нахождения вершины графика. Возьмем формулу для координаты x-вершины: x = -b/(2a). В нашем случае, a = 1, b = -2, поэтому x = -(-2)/(2*1) = 2/2 = 1. Значит, вершина графика находится в точке с координатами (1, y).
2. Теперь найдем y-координату вершины, подставив x = 1 в уравнение функции: y = 1² - 2*1 + 3 = 1 - 2 + 3 = 2. Таким образом, вершина графика имеет координаты (1, 2).
3. Далее, нам понадобится знать, как растягивается или сжимается график функции. Если a > 0, то график функции открывается вверх, и если a < 0, то график функции открывается вниз. В нашем случае a = 1, поэтому график открывается вверх.
4. Наконец, для построения графика обойдемся несколькими точками. Подставим несколько различных значения x в уравнение функции, чтобы найти соответствующие значения y. Например, если x = 0, то y = 0² - 2*0 + 3 = 3. Таким образом, у нас есть точка (0, 3). Если x = 2, то y = 2² - 2*2 + 3 = 4 - 4 + 3 = 3. Это означает, что у нас есть вторая точка (2, 3).
5. Нарисуем полученные точки на графике и проведем плавную кривую линию через них. График будет иметь вид увенчанного вершиной параболы ветвями, направленными вверх.
Теперь, чтобы узнать номер рисунка, на котором изображен график функции y=x²-2x+3, мы должны сопоставить полученный график с предложенными вариантами. Ответ будет номером рисунка, на котором график совпадает с тем, что мы построили.
ответ: Рисунок номер 1
Координаты вершины параболы:
x =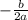
= - (2 ÷ 2) = 1
y = 1 - 2 × 1 + 3 = 2
ответ: первый рисунок