 ,
, , a
, a 
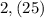
 целая часть. У нас она равна 2
целая часть. У нас она равна 2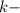 - количество цифр в периоде. У нас их 2
- количество цифр в периоде. У нас их 2 количество цифр до периода. У нас их 0
количество цифр до периода. У нас их 0 все цифры, включая период, в виде натурального числа. У нас это 25
все цифры, включая период, в виде натурального числа. У нас это 25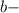 все цифры без периода в виде натурального числа. Их нет.
все цифры без периода в виде натурального числа. Их нет.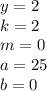
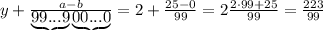
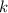 подставляется количество 9, а под
подставляется количество 9, а под  -количество нулей. У нас
-количество нулей. У нас 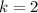 , значит пишем две цифры 9, а
, значит пишем две цифры 9, а  , значит, нулей не пишем вообще. Между
, значит, нулей не пишем вообще. Между 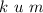 не стоит знак умножения
не стоит знак умножения
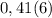
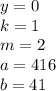

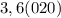

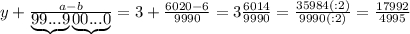
Объяснение:
1) (a-5)(a+3) < (a+1)(a-7)
a^2-5a+3a-15 < a^2+a-7a-7
-2a-15 < - 6a-7
4a < 8
a < 2
Это неравенство верно вовсе не при любых а, а только при а меньше 2.
2) [5x+2] <= 3
Видимо, квадратные скобки это модуль. Неравенство распадается на два:
а) 5x+2 >= - 3
5x >= - 5
x >= - 1
б) 5x+2 <= 3
5x <= 1
x <= 1/5
Целые решения: - 1; 0
3) Пусть одна сторона равна 5 см, а другая больше неё в 4 раза, то есть 20 см.
Тогда периметр равен 2*(5+20) = 2*25 = 50 см.
Если первая сторона меньше 5 см, то вторая меньше 20 см, а периметр меньше 50 см.
Пусть v катера будет х, а v течения реки будет у. Если катер часа по течению, то за это время он расстояние: (х+у)3. Когда он проходил по озеру, то находился в стоячей воде без течения и расстояние 3х. За 6 часов он расстояние 114км, и теперь составим уравнение:
(х+у)3+3х=114. Разберём вторую часть задачи. Катер против течения 4 часа, поэтому за это время он х-у)4. Так как он расстояние на 10 км больше, чем за 3 часа по озеру, то по озеру он пройдёт 2х и разница составляет 10км. По этим данным составим второе уравнение:
(х-у)4-3х=10. Решим систему уравнений:
{(х+у)3+3х=114
{(х-у)4-3х=10
{3х+3у+3х=114
{4х-4у-3х=10
{6х+3у=114 |÷3
{х-4у=10
{2х+у=38
{х=10+4у.
Подставим эти значения в первое уравнение:
2х+у=38
2(10+4у)+у=38
20+8у+у=38
9у=38-20
9у=18
у=18÷9
у=2; итак v течения реки=2км/ч
Теперь подставим в уравнение значение у:
х=10+4у
х=10+4×2=10+8=18км/ч.
ответ: v катера=18км/ч;
v течения реки=2км/ч