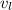. Найдём скорость легкового автомобиля: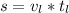
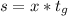
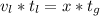
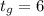часов (2ч+4ч=6ч)
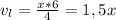(км\ч).
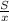, а время, затраченное на прохождение всего пути, легковым автомобилем равно 
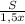. Но т.к. легковой автомобиль потратил на дорогу на 1 час меньше времени чем грузовик, к тому же выехал на 2 часа позже, то можно записать следующее выражение: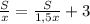
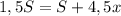
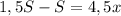
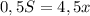
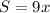
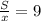часов
1 машина 216 км х км/ч 216/х час
2 машина 252 км у км/х 252/у час
216/х - 252/у = 1
216/х + 252/у = 4 1/3
Решаем эту систему. Обозначим 216/х = t, 252/у = z
наша система: t - z = 1
t + z = 13/3 сложим:
2t = 16/3
t = 8/3
t - z = 1
8/3 -z =1
z = 8/3 -1
z = 5/3
Возвращаемся к нашей подстановке:
а) 216/х = 8/3 ⇒ х = 216·3: 8 = 63,5(км/ч) - V1
б) 252/у = 5/3 ⇒ у = 252·3:5= 153,2(км/ч) - V2