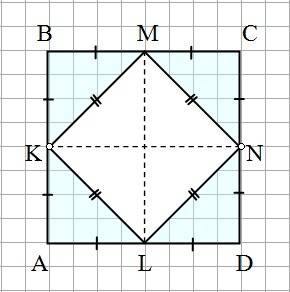
Докажите, что середины сторон квадрата являются вершинами другого квадрата.
1). Рассмотрим треугольники в углах исходного квадрата, - KBM; MCN; NDL; LAK. Все они являются равнобедренными прямоугольными треугольниками с равными катетами.
Следовательно, их гипотенузы также равны: KM = MN = NL = LK.
Кроме того, так как углы при гипотенузах равны 45°, то:
∠KMN = ∠MNL = ∠NLK = ∠LKM = 90°
Получили:
KMNL - ромб с углами по 90° => KMNL является квадратом.
2). Проведем в четырехугольнике KMNL диагонали ML и KN.
Так как BK = CN = AK = ND, то ВС || KN || AD
Аналогично: AB || ML || CD.
Следовательно: ML⊥KN, причем: ML = KN.
Значит KMNL - ромб с равными диагоналями, т.е. KMNL - квадрат.
Точка А имеет координаты (-1/2;-10)
Первое число в скобках - это значение x, а второе число в скобках это значение y, подставив значения 1)y=5/-0,5=-10, значения сходятся, значит, принадлежит.
2)Подставив, по такому же принципу - да
3)Нет.
Пояснения: в первом примере, чтобы разделить на десятичную дробь, нужно перенести запятую, а сверху к числу добавить ноль, то есть у нас получилось вот что: 50/-5=-10, так как делим положительное число на отрицательное, а если делить отрицательное число на отрицательное число, получится положительное число, проще говоря, минус на минус дадут плюс, если есть вопрос по решению - спроси :)
a) 2/3-(x-1/21)=2/7
х-1/21=2/3-2/7
х=14/21-6/21+1/21
х=15/21-6/21
х=9/21
х=3/7
b) (3/8-x)-1/5=1/20
3/8-х=1/20+1/5
х=3/8-1/20-1/5
х=15/40-2/40-8/40
х=15/40-10/40
х=5/40
х=1/8
в) 3/5x+3/20x+1/4x=2/7
12/20х+3/20х+5/20х=2/7
20/20х=2/7
х=2/7
г) 2/3-(5/6-x)=1/12
5/6-х=2/3-1/12
х=5/6-2/3+1/12
х=10/12-8/12+1/12
х=11/12-8/12
х=3/12
х=1/4