Question

Решите показательные уравнения и неравенства.

Answer 1

1)$0,3^{3 - 2x}=0,09$

$0,3^{3 - 2x}=0,3^{2}$

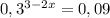
Т.к. основания степеней равны ⇒ степени тоже равны

3-2x=2

3-2=2x

2x=1 | : 2

x=0,5

ответ: x=0,5

2)$3^{x-2} - 3^{x-3} = 2$

$3^{x-3}*(3^{1} - 3^{0}) = 2$

$3^{x-3}*(3 - 1) = 2$

$3^{x-3}*2 = 2$ | : 2

$3^{x-3} = 1$

$3^{x-3} = 3^{0}$

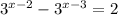
Т.к. основания степеней равны ⇒ степени тоже равны

x-3=0

x=3

ответ: x=3

3)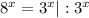$8^{x}=3^{x} | : 3^{x}$ ( имеем право т.к. $3^{x}$ ≠ 0)

$\frac{8^{x} }{3^{x} } =1$

$(\frac{8}{3})^{x} = 1$

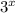$(\frac{8}{3})^{x} = (\frac{8}{3})^{0}$

Т.к. основания степеней равны ⇒ степени тоже равны

x=0

ответ: x=0

4)$25^{x}+4*5^{x} - 5 = 0$

$5^{2x}+4*5^{x} - 5 = 0$

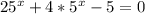
Пусть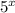 $5^{x}$=t, тогда:

$t^{2} +4t-5=0$

D = 4²-4*1*(-5)=16+20=36=6²

$t_{1} = \frac{-4+6}{2*1} = \frac{2}{2}=1$

$t_{2} = \frac{-4-6}{2*1} = - \frac{10}{2}= -5$ - посторонний корень (т.к. число в любой степени не является отрицательным)

Вернёмся к замене:

$5^{x}=1$

$5^{x}=5^{0}$

Т.к. основания степеней равны ⇒ степени тоже равны

x=0

ответ: x=0

5)$(\frac{1}{3}) ^{x} (\frac{1}{27}) ^{7}$

$(\frac{1}{3}) ^{x} (\frac{1}{3}) ^{3*7}$

$(\frac{1}{3}) ^{x} (\frac{1}{3}) ^{21}$

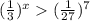
Т.к. основания степеней равны ⇒ степени тоже равны, НО

Основания степеней < 1 ⇒знак меняем

x<21

ответ: x<21

Answer 2

1) $0,3^3^-^2^x=0,09$

$(\frac{3}{10}) ^3^-^2^x=(\frac{3}{10} )^2$

$3-2x=2$

$-2x=2-3$

$-2x=-1$

$x=\frac{1}{2}$

2)$3^x^-^2-3^x^-^3=2$

$(3-1)*3^x^-^3=2$

$2*3^x^-^3=2$

$3^x^-^3=1$

$3^x^-^3=3^0$

$x-3=0$

$x=3$

3)$8^x=3^x$

$(\frac{8}{3} )^x=1$

$(\frac{8}{3} )^x=(\frac{8}{3} )^0$

$x=0$

4)$25x+4*5^x-5=0$

$(5^2)+4*5^x-5=0$

$(5^x)^2+4*5^x-5=0$

$t^2+4t-5=0$

$t=-5$

$t=1$

$5^x=-5$

$5^x=1$

$x\neq R$

$x=0$

5)$(\frac{1}{3} )^x(\frac{1}{27} )^7$

$3^-^x3^-^2^1$

$-x-21$

$x$

x∈(-∞,21)