представим в таком виде: 0< 1/4 * x^2 <1
тогда видим что все части можно умножить на 4: 0<x^2<4
теперь разделим неравенство на два неравенства: x^2>0
и x^2<4
решаем первое: x^2>0
x не равно 0
решаем второе: x^2<4
x^2 - 4<0
(x-2)(x+2)<0
-2<x<2 или (-2;2)
соединим оба решения и получим ответ: (-2;0) и (0;2)
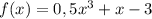
Рассмотрим данную функцию:
1)Она непрерывная на всей числовой прямой и принимает как положительные f(2)=3,так и отрицательные f(0)=-3 значения,а значит как минимум один раз обращается в 0-пересекает ось абсцисс(то есть уравнение имеет по-крайней мере 1 действительный корень)
2)Рассмотрим производную этой функции:
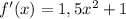
Она принимает только положительные значения(думаю это очевидно),а значит функция возрастает на всей своей области определения(коей является вся числовая прямая) и может пересечь ось абсцисс не более 1 раза.
Вывод исходное уравнение имеет ровно 1 действительный корень.
P.S.Можно доказать,используя теореу Штурма(но это уже не школьная программа),если надо допишу этот метод.
( t+2)/4 = (3t−4)/11
11 t+22 = 12t−16
t=6
Если воспринять так уравнение t+2/4 = 3t−4/11⇒2t=2/4+4/11; 2t=2/4+4/11
2t=38/44; t=19/44;