1. Найдите сумму бесконечно убывающей геометрической прогрессии 36: 12; 4; ...;
b1=36
b2=12
b3=4
q=b2/b1
s=b1/(1-q)
q=-12/36=-1/3
s=36/(1+1/3)=36/(4/3)=36*3/4=27
ответ: 27
2. Сумма бесконечно убывающей геометрической прогрессии равна 54. Найти, если
Если...? Тут как будто какого-то условия не хватает ((
3. Найдите сумму и первых членов арифметической прогрессии, если а=1, an=200, n=100
Sn = (a1 + an)/2* n
a1 = 1
an = 200
n = 100
S100 = (1 + 200)/2*100 = 201*50 = 10050
ответ: 10050
Объяснение:
Проверь второе задание, там будто реально условия не хватает.
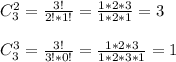
Вот решил 2 задачи. Вроде бы все правильно