возьмем к примеру
1 сорт- 1
2 сорт-2
3 сорт-3
4 сорт-4
5 сорт-5
мы можем взять
1 и 2, 1 и 3 , 1 и 4 , 1 и5 ,2 и 3,2 и 4, 2и5, 3 и 4 , 3и5 ,4 и
Того мы можем купить 2 буханки
для этого еблана в Задача 1. Дві прямі АВ і СД перетинаються в
точці О, утворюють кут ДОВ, який дорівнює 40
градусів. Визначте величину решти кутів, що
утворилися при перетині прямих АВ і СД.
Задача 2. Один з кутів, утворених при перетині
двох прямих, прямий. Чому дорівнює решта
Объяснение:
Задача 1. Дві прямі АВ і СД перетинаються в
точці О, утворюють кут ДОВ, який дорівнює 40
градусів. Визначте величину решти кутів, що
утворилися при перетині прямих АВ і СД.
Задача 2. Один з кутів, утворених при перетині
двох прямих, прямий. Чому дорівнює рештаЗадача 1. Дві прямі АВ і СД перетинаються в
точці О, утворюють кут ДОВ, який дорівнює 40
градусів. Визначте величину решти кутів, що
утворилися при перетині прямих АВ і СД.
Задача 2. Один з кутів, утворених при перетині
двох прямих, прямий. Чому дорівнює решта
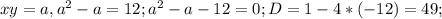
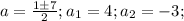, вот теперь мы можем заменить первое уравнение на более простое и решить 2 системы, объединив их решения.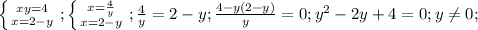 
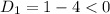, корней нет. Решаем вторую систему: 
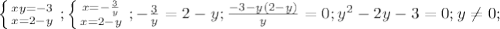Здесь b=a+c (-2=1-3), тогда 
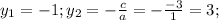, а теперь в любое уравнение подставляем каждое из получившихся и в ответе пишем 2 точки: 
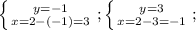, получили точки (3;-1);(-1;3). Довольно похожие значения, объясняется это всё квадратами в первом уравнении системы. ответ:(3;-1);(-1;3).
ответ: мы можем взять 2 буханки 10 различными