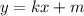 : если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором
: если k>0, функция возрастает, k<0 - убывает. Всё просто. Т.е. в убывании обе функции линейные, k<0 и в первом (k=-7), и во втором 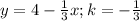 . С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения
. С этим разобрались. Теперь к возрастанию. Я не знаю, в каком Вы классе, постараюсь объяснить доступно. Чтобы определить возрастание/убывание функции, нужно взять значения 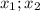 , два произвольных числа, но
, два произвольных числа, но 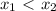 . Пусть мы имеем функцию
. Пусть мы имеем функцию  , тогда вычисляем значения функции в этих двух точках, имеем
, тогда вычисляем значения функции в этих двух точках, имеем 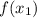 и
и 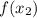 , так вот, если
, так вот, если  , тогда функция возрастающая, если же
, тогда функция возрастающая, если же 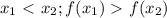 , то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)
, то она убывающая, но только ПРИ УСЛОВИИ, что она монотонна на всей области определения (т.е. ТОЛЬКО возрастает или ТОЛЬКО убывает), в противном случае мы говорим о ПРОМЕЖУТКАХ возрастания и убывания. 1)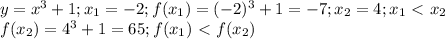 , т.е. функция возрастающая. А вот задание с
, т.е. функция возрастающая. А вот задание с 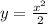 не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной)
не совсем корректно, так как эта функция возрастает только при x>0, при x<0 она убывает, x=0 - Точка экстремума. Если уж брать математический анализ, то легко взять производную и исследовать функцию на "скорость изменения" (алгебраический смысл производной) 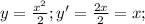 . Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка):
. Если производная в некоторой точке отрицательная, то функция убывает, если производная положительная, то функция возрастает, если производная равна 0, то это точка экстремума. Очевидно, что при x<0 функция убывает, при x>0 возрастает. Если же доказывать возрастание на промежутке x>0, тогда действуем, как и в первом случае (только не берем значения из ненужного нам промежутка): 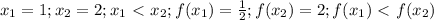 , функция возрастает, что и требовалось доказать.
, функция возрастает, что и требовалось доказать.
Если на одной из двух прямых отложить последовательно равные отрезки и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
По условию четыре данные прямые параллельны, отсекают на прямой ЕН отрезки, равные длине отрезка ЕF, т.е. 6 см.
Значит, ЕН=3•6=18 см
CD=CB=AB=4, и AD=3•4=12 см
Проведем параллельно AD прямую ЕМ, пересекающую параллельные прямые СF и BG в точках Т и К соответственно.
СТ=ВК=АМ=DE=51 см.
ТF=CF-51=57-51=6 см,
Соответственные углы при пересечении параллельных прямых секущими равны (свойство), ⇒
∆ ТЕF, ∆ KEG и ∆ МЕН подобны;
TF - средняя линия ∆ КЕG ⇒ KG=2•TF=12 см
BG=51+12=63 см
КT=КМ=ТЕ=4
У подобных ∆ ТЕF и ∆ МEН k=EH:EF=18:6=3⇒
MH=6•3=18 см
Итак, АD=3•4=12 см,
EH=18 см
DE=51; CF=57 см
AH=51+18=69 см
Нужно металлических прутьев
12+18+57+63+69+51=30+120+120=270 cм =2,7 м
Мастер хорошо знает геометрию и применяет ее в своей работе.
Объяснение:
не мне а Hrisula это он решил.