Задание 1. Правописание наречий объяснить графически (обозначьте
суффиксы и приставки наречий). Объяснить правописание наречия.
Определить его разряд. Налев..., Когда (нибудь), Свеж..., Сгоряч...
Задание 2. Образуйте степени сравнения наречий. Наречие сравнительная. Составная сравнительная, превосходная степень: холодно,
мало, полезно.
Задание 3. Вставьте подходящие по смыслу наречия или прилагательные в
сравнительной степени. Сегодня день.. Девочка оделась.. Вторая работа
написана..
Объяснение:
Задание 1. Правописание наречий объяснить графически (обозначьте
суффиксы и приставки наречий). Объяснить правописание наречия.
Определить его разряд. Налев..., Когда (нибудь), Свеж..., Сгоряч...
Задание 2. Образуйте степени сравнения наречий. Наречие сравнительная. Составная сравнительная, превосходная степень: холодно,
мало, полезно.
Задание 3. Вставьте подходящие по смыслу наречия или прилагательные в
сравнительной степени. Сегодня день.. Девочка оделась.. Вторая работа
написана..
Возможно, существует и другой метод доказательства, но я буду использовать метод от противного.
Итак, нужно доказать, что 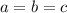 , то есть
, то есть
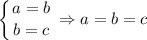
Перепишем наше равенство, переместив все в левую часть:
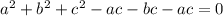
1) Предположим, что 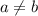 (при этом подразумевая, что
(при этом подразумевая, что 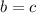 )
)
Тогда получаем следующее:
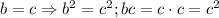
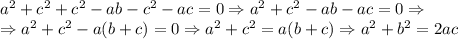
Далее смотрим: слева неотрицательное выражение всегда, а справа может быть и отрицательное, но у нас по условию дано, что для любых действительных чисел равенство выполняется, а здесь это далеко не так (на языке математики запись такая: 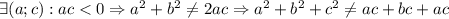 )
)
Возможно, это не очень явно, поэтому вспомним, что по предположению 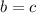 , и доделаем:
, и доделаем:
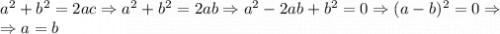
А это прямо яркий пример противоречия: предположив, что 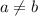 , мы получили
, мы получили 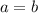 .
.
Из этого следует, что 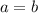 , но и из предположенного же
, но и из предположенного же 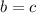 уже следует, что
уже следует, что 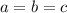 .
.
Вообще, по идее, этого уже достаточно, ну на всякий случай посмотрим ещё:
2) Предположим, что 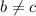 (при этом
(при этом 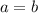 )
)
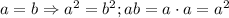
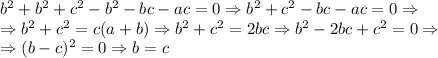
И тогда уже точно исходя из пунктов 1) и 2), получаем
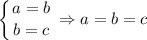 , что и требовалось доказать.
, что и требовалось доказать.
апапар
Объяснение:
опрор
4 угол