1. Обратно пропорциональная зависимость :
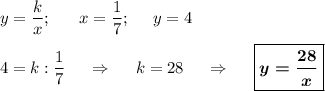
2. Решите графически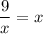 
График функции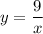 
- гипербола в первой и третьей четвертях (k=9>0). Точки для построения :
x -9 -4,5 -3 -2 -1 1 2 3 4,5 9
y -1 -2 -3 -4,5 -9 9 4,5 3 2 1
График функции y = x - прямая линия, проходящая через начало координат. Точки для построения
x 0 2
y 0 2
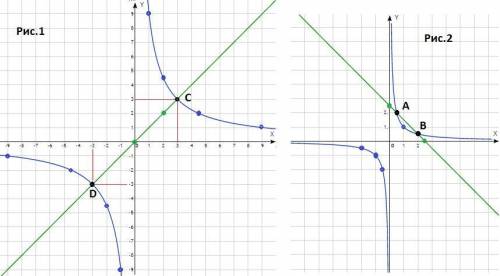
ответ : (-3; -3) и (3; 3) - рис. 1.
3. Графически, сколько решений имеет уравнение 
График функции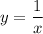 
- гипербола в первой и третьей четвертях (k=1>0). Точки для построения :
x -2 -1 -0,5 0,5 1 2
y -0,5 -1 -2 2 1 0,5
График функции y = 2,5 - x - прямая линия. Точки для построения
x 0 2,5
y 2,5 0
ответ : уравнение имеет 2 решения - рис. 2.
ответ:1) Задание
Дана функция
найти промежутки возрастания и убывания
По признаку возрастания и убывания функции на интервале:
если производная функции y=f(x) положительна для любого x из интервала X, то функция возрастает на X;
если производная функции y=f(x) отрицательна для любого x из интервала X, то функция убывает на X.
Найдем производную данной функции
найдем точки экстремума, точки в которых производная равна нулю
отметим точки на числовой прямой и проверим знак производной на промежутках
___+-+__
0 2
Значит на промежутках (-оо;0) ∪ (2;+оо) функция возрастает
на промежутке (0;2) функция убывает
точки х=0 точка минимума, х=2 точка максимума
Найти наибольшее и наименьшее значение функции на отрезке [-2; 1].
Заметим, что х=2 точка максимума не входит в данный промежуток,
а х=0 принадлежит данному промежутку
Проверим значение функции в точке х=0 и на концах отрезка
Значит наибольшее значение функции на отрезке [-2;1]
в точке х=0 и у(0)=1
значит наименьшее значение функции на отрезке [-2;1]
в точке х=-2 и у(-2)= -19
2. Напишите уравнение к касательной к графику функции
f(x)=x^3-3x^2+2x+4 в точке с абсциссой x0=1.
Уравнение касательной имеет вид
найдем производную данной функции
найдем значение функции и производной в точке х=1
подставим значения в уравнение касательной
Объяснение: