Решите задачу
Из двух пунктов, расстояние между которыми 81 км, выехали одновременно навстречу друг другу два велосипедиста и встретились через 3 ч. Известно, что скорость первого велосипедиста на 3 км/ч больше скорости второго. Определите скорость каждого велосипедиста. Заполните пропуски и закончите решение задачи.
Решение: Пусть скорость первого велосипедиста x км/ч, а второго — y км/ч. За 3 ч первый велосипедист проехал
км , а второй —
км. Велосипедисты вcтретились, значит, вместе они проехали 81 км. Следовательно,
. Скорость первого велосипедиста на 3 км/ч больше скорости второго, следовательно,
. Из уравнений 1 и 2 составим систему
ответы вносите в порядке возрастания
ответ:
км/ч,
км/ч.
Если в ответе десятичная дробь, то запишите её через запятую. Если в ответе обыкновенная дробь, то запишите её в несократимом виде через черту /. Если в ответе смешанная дробь, то запишите целую часть через пробел от дробной: -5 1/2
 ;
;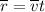 ;
;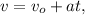 либо в векторном виде:
либо в векторном виде: 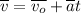 ;
;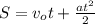 либо в векторном виде:
либо в векторном виде: 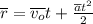 ;
;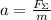 либо в векторном виде:
либо в векторном виде: 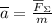 ;
; ;
;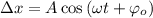 ;
;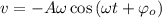 ;
; ;
;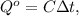 где
где 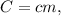 либо в удельном виде:
либо в удельном виде:  ;
;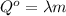 ;
;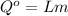 ;
; ;
; ;
;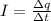 ;
;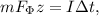 где
где  ;
;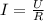 ;
;
 ;
; ;
; ;
;
a³+3a²+2a=a(a²+3a+2)=a(a+1)(a+2)
a²+3a+2=(a+1)(a+2)
D=3²-4*1*2=9-8=1
a₁=(-3+1)/2=-2/2=-1
a₂=(-3-1)/2=-4/2=-2
В итоге, мы получили произведение трёх подряд идущих чисел, среди которых обязательно найдётся хотя бы одно чётное число и число делящееся на три. Следовательно, произведение трёх подряд идущих чисел будет кратно 6. Т.к. итоговое произведение получено из исходного многочлена путём равносильных преобразований, то делаем вывод:
многочлен а³+3а²+2а кратен числу 6.