Нет, нельзя. Сокращать можно только множители
26,
т.к. по условию в графу ответа надо писать
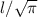
Объяснение:
Из условия ни разу не ясно, что есть такое некая непонятная "его длина".
Но по всей видимости,
а) это диаметр условной окружности, которую образует Кольцевая линия.
б) это (ну, блин, грамотеи!) длина окружности, которую образует Кольцевая линия.
а) Найдем диаметр условной окружности, которую образует Кольцевая линия.
Обозначим её как d.
Площадь Центрального района S можно вычислить следующим образом:
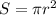
где r - это радиус условной окружности Кольцевой, или половина диаметра, т.е. d/2. Отсюда.
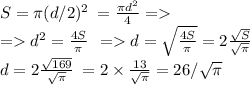
б) Найдем длину окружности, которую образует Кольцевая линия. Обозначим её как l.
Длина окружности равна
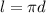
где d - условный диаметр (см. (а)).
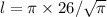
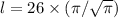
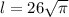
Согласно требованиям задачи в ответ записываем
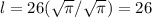
т.е.
ответ: 26
№1
Пусть x-скорость лодки по течению, тогда y-скорость лодки против течения. Составим систему уравнений:
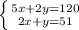
Домножим нижнее уравнение на -2
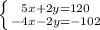
Решим методом сложения:
5x+2y-4x-2y=120-102
x=18
Подставим значение х во второе уравнение и найдем y:
2*18+y=51
36+y=51
y=51-36
y=15
Пусть скорость течения-x, а скорость лодки - y. Составим систему уравнений:
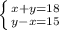
Решим методом сложения
x+y+y-x=32
2y=32
y=32/2
y=16
Подставим значение y в первое уравнение и найдем x:
x+16=18
x=18-16
x=2
ответ: скорость течения реки- 2км/ч. скорость лодки - 16 км/ч
№2
Пусть x- возраст отца, y-возраст сына
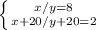
Выразим x из первого уравнения:
x/y=8
x=8y
Подставим значение x во второе уравнение:
8y+20/y+20=2
Перемножим методом креста:
2y+40=8y+20
-6y=-20
y=20/6
Выразим x:
x=8*20/6
x=80/3
Прибавим по 20 к x и y
x+20=80/3+20=140/3=46
y+20=20/6+20=140/6=23
ответ: Сыну 23 года, Отцу 46 лет.
Объяснение:
Термин "сократить" употребляется только для сокращения МНОЖИТЕЛЕЙ. В числителе заданной дроби стоит выражение, которое называется алгебраическая СУММА, но не произведение. Поэтому ничего нельзя сокращать.
Причём в этой сумме есть слагаемое, которое представляет из себя произведение (2х+1)(х+1) , но всё же оно СЛАГАЕМОЕ, но не произведение. Если бы числитель был полностью разложен на множители, то тогда сократить можно было бы одинаковые МНОЖИТЕЛИ.
Здесь можно было почленно разделить слагаемые числителя на знаменатель, и тогда появиться дробь, где в числителе будет стоять произведение, в котором одним из множителей будет (2х+1) , который есть и в знаменателе. Вот в этой дроби и можно сократить одинаковые множители.