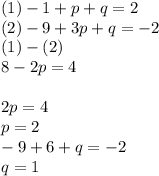
получим
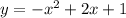
найдем производную
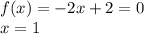
ветви направлены вниз, т.к а <0
тогда, (-беск; 1) возрастает
(1; +беск) убывает
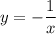и затем верхнюю часть графика отобразить в нижнюю(отрицательную часть)
(*)
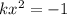и это уравнение решений не имеет при k>0(так как левая часть всегда положительно).
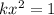и при k<0 это уравнение решений не имеет.
, имеем
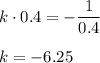
Исследуйте на четность функцию :
1) y = f(x) = - 8x + x² + x³
2) y = f(x) = √(x³ + x²) - 31*| x³ |
ни четные ,ни нечетные
Объяснение:
1)
f(x) = - 8x + x² + x³ ; Область Определения Функции: D(f) = R
функция ни чётная ,ни нечётная
проверяем:
Функция является четной, когда f(x)=f(-x) , нечетной, когда f(-x)=-f(x)
а) f(-x) = - 8*(-x) +(- x)² +(- x)³ = 8x + x² - x³ ≠ f(-x)
Как видим, f(x)≠f(-x), значит функция не является четной.
б)
f(-x) ≠ - f(-x) → функция не является нечетной
- - - - - -
2)
y = f(x) = √(x³ + x²) - 31*| x³ | ,
D(f) : x³ + x² ≥ 0 ⇔ x²(x+1) ≥ 0 ⇒ x ≥ -1 * * * x ∈ [ -1 ; ∞) * * *
ООФ не симметрично относительно начало координат
* * * не определен , если x ∈ ( -∞ ; - 1) * * *
функция ни чётная ,ни нечётная
Подставим точки в уравнение получим систему для нахождения коэффициентов квадратичной функции
2=-1+р+q
-2=-9+3р+q
Вычтем из первого уравнения второе, получим
0=8-2р
откуда р=2 найдем q=3-р=3-2=1
уравнение имеет вид у=-х²+2х+1
Абсцисса вершниы параболы равна -2/-2=1
Первый коэффициент равен минус единицы, поэтому парабола направлена ветвями вниз, и возрастает на промежутке (-∞;1]; убывает на промежутке [1;+∞)