Мы делаем предположение, что то, что нам дано неверно, к примеру:
Доказать иррациональность числа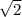 
Допускаем противное, что число 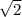- рациональное, после чего уже доказываем что наше предположение не верно, в примере с корнем:
Любое рациональное число можно представить как несократимую дробь, где числитель - целое число, а знаменатель - натуральное
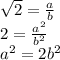
Отсюда следует, что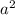 
чётно, значит, чётно и a; следовательно, 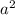делится на 4, а значит,
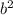и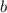 
тоже чётны. Полученное утверждение противоречит несократимости дроби 
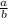. Это противоречит изначальному предположению и 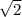- иррациональное число.
только есть нюанс -числа целые (а не натуральные)))
1) для четного целого n утверждение очевидно:
n = 2k, k∈Z (2k)² - 5(2k) + 2 = 2*(2k² - 5k + 1)
2) для НЕчетного целого n:
n = 2k+1, k∈Z
(2k+1)² - 5(2k+1) + 2 = 4k² + 4k + 1 - 10k - 5 + 2 = 2*(2k² - 3k - 1)
для чисел, кратных трем, будет на один вариант больше представлений:
n = 3k (число кратно трем)
n = 3k+1 (число НЕ кратно трем --дает остаток 1)
n = 3k+2 (число НЕ кратно трем --дает остаток 2)
1) (3k)³ + 2(3k) - 3 = 3*(9k³ + 2k - 1)
2) (3k+1)³ + 2(3k+1) - 3 = 27k³ + 27k² + 9k + 1 + 6k + 2 - 3 =
= 3*(9k³ + 9k² + 3k)
3) (3k+2)³ + 2(3k+2) - 3 = 27k³ + 54k² + 36k + 8 + 6k + 4 - 3 =
= 3*(9k³ + 18k² + 14k + 3)
можно было доказывать и в первом и во втором случае кратность только для первых двух слагаемых, т.к. третьи слагаемые в обоих случаях кратны заданным числам... чуть короче бы получилось...