Складываем оба уравнения, получим:
x² - 2 * x * y + y² = 1.
Разложим по формуле квадрата разности, получим:
(x - y)² = 1,
x - y = 1,
x - y = -1.
Вычитаем из первого системного уравнения второе, получим:
x² - y² = 3.
Разложим как разность квадратов, получим:
(x - y) * (x + y) = 3.
Следовательно, получим две системы уравнений:
1. (x - y) * (x + y) = 3 и x - y = 1,
x + y = 3 и x - y = 1.
Складываем почленно:
2 * x = 4, откуда х = 2,
y = x - 1 = 2 - 1 = 1.
2. (x - y) * (x + y) = 3 и x - y = -1,
x + y = -3 и x - y = -1,
2 * x = -4,
x = -2,
y = x + 1 = -2 + 1 = -1.
ответ: (2; 1) и (-2; -1).
Объяснение:
1) (x+2)²(x-5)^3=(x-5)(x+2)^4
(x+2)²(x-5)^3-(x-5)(x+2)^4=0
(x+2)²(x-5)((x-5)²-(x+2)²)=0
(x+2)²(x-5)((x-5-(x+2))((x-5+(x+2))=0
(x+2)²(x-5)·(-7)(2x-3)=0
-14(x+2)²(x-5)(x-1,5)=0
(x+2)²(x-5)(x-1,5)=0
x= -2; 1,5; 5;
ответ: -2; 1,5; 5;
2) (2x+1)^3(2x-3)^5=(2x+1)^5(2x-3)^3
(2x+1)^3(2x-3)^5-(2x+1)^5(2x-3)^3=0
(2x+1)^3(2x-3)^3((2x-3)^2-(2x+1)^2)=0
(2x+1)^3(2x-3)^3((2x-3)-(2x+1))((2x-3)+(2x+1))=0
(2x+1)^3(2x-3)^3·(-4)(4х-2)=0
-16· (2x+1)^3(2x-3)^3(х-0,5)=0
(2x+1)^3(2x-3)^3(х-0,5)=0
8·8(x+0,5)^3(x-1,5)^3(х-0,5)=0
(x+0,5)^3(x-1,5)^3(х-0,5)=0
х= -0,5; 0,5; 1,5;
ответ:-0,5; 0,5; 1,5;
Объяснение:
Дано:
2(5x−22)2−6(5x−22)+4=0
Выполним замену: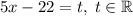
Обратная замена:
Произведение равно 0, когда хотя бы 1 из его множителей равен 0, а другой при этом не теряет смысла:
Уравнение решено.