При каких значениях параметра а уравнение |x2 – 4|x|| = a имеет четыре решения?
у = |x2 – 4|x|| у = a
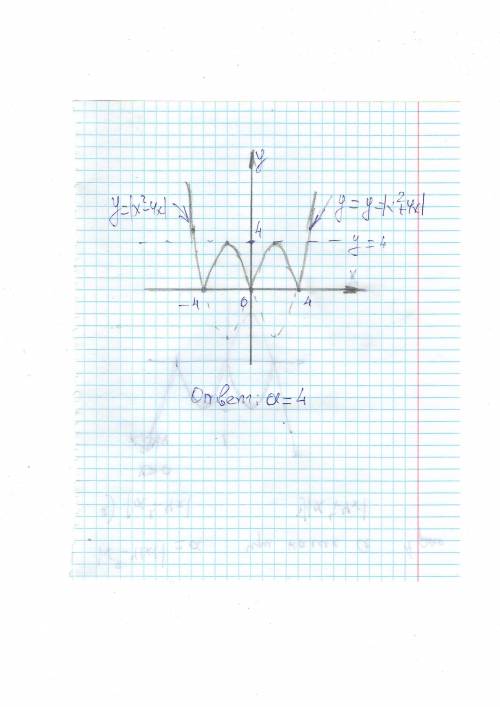
Прямая у = а должна пересечь у = |x2 – 4|x|| в 4-х точках
у = |x2 – 4|x||
а) х ≥ 0 б) x < 0
у = |x2 – 4x| у = |x2 + 4x|
парабола с корнями 0 и 4 парабола с корнями 0 и -4
остальное в приложении
Объяснение:
2/6, 2/3 шукаємо найбільший спільний множник (нсм). шукаємо число, яке ділиться на 6, і на 3. це буде 6. 6:6=1, 6:3=2. до першого дробу, зверху пишемо 1, тому що результат 6:6=1. до другого дробу, зверху пишемо 2, тому що результат 6:3=2. у першому дробі, 2•1=2. тобто, число написане зверху, множимо на чисельник (число те, що зверху). у другому дробі 2•2=4, робимо те же саме, що робили і в першому дробі. записані результати записуємо: 2/6, і 4/6. в знаменник в результаті записуємо те число, яке стало найбільшим спільним множником. сподіваюся, що до
Для острых углов известно соотношение sinα<α<tgα . α=1/(n+6) стремится к 0 при n->∞.
tg1/(n+6)>1/(n+6).
Исходный ряд сравним с рядом ,общий член которого 1/(n+6).Этот ряд расходящийся, так как его можно сравнить с расходящимся обобщённо-гармоническим рядом ∑1/n : lim (1/n)/(1/n+6)=1≠0 при n->∞ ⇒ оба ряда ∑1/n и ∑1/(n+6) расходятся.
Ряд ∑1/(n+6) является минорантным, а ряд ∑tg1/(n+6) мажорантным. Из расходимости минорантного ряда следует расходимость мажорантного. ⇒∑tg1/(n+6) - расходящийся ряд.
При a=4
Объяснение:
Если перенести а в левую сторону, получим обычное квадратное уравнение из четырех вариантов с + и - аргументов под модулем.
Чтоб у каждого было по одному решению, дискриминант в каждом случае должен быть 0.
Это возможно только при а=4