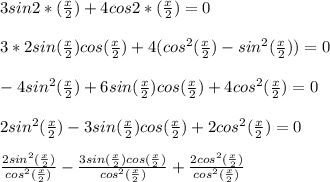 =0
=0
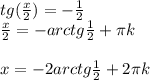 ,
,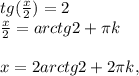
 k∈Z;
k∈Z;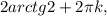 k∈Z.
k∈Z.
Что вы понимаете под словом упростить? И где уравнение-то само?
Если упростить = записать в виде многочлена в стандартной форме, то все ок. Если хочется раскладывать на множители, то это можно делать методом неопределенных коэффициентов.
Пусть исходный многочлен - произведение 2 квадратных трехленов (x^2+ax+b)(x^2+px+q)
Дальше приравниваем коэффициенты при равных степенях.
0 = a + p
2 = q + ap + b
-3 = bp + aq
1 = bq
Из первого p=-a. Из последнего q=1/b.
2 = 1/b - a^2 + b
-3 = -ab + a/b
Дальше можно, например, выразить a из первого и из второго
a^2 = 1/b + b - 2 = (b^2 - 2b + 1)/b=(b-1)^2 / b
a = 3/(1-1/b) = 3b / (b-1)
9b^2/(b-1)^2 = (b-1)^2 / b
9b^3 = (b-1)^4
и дальше все очень нехорошо.
Впрочем, можно понять, что и этого многочлена нет корней. Например, привлекая производную. Производная равна 4x^3+4x-3. Например, по второй производной можно понять, что у производной только 1 ноль, заключенный между 0 и 1. Для таких иксов x^2+2x^2-3x+1>x^2+2x^2+1>=0.
При разложении на множители можно вспользоваться и таким утверждением: если многочлены совпадают на каком-то промежутке, то они совпадают везде. В частности, при x>0 можно применять разность квадратов.
x^4 + 2x^2 - 3x + 1 = (x^2 + 1)^2 - 3x = (x^2+1-sqrt(3x))(x^2+1+sqrt(3x))
Теперь имеем относительно t = sqrt(x) уже кубические многочлены (впрочем
, особой радости от этого нет - все равно отсюда ничего путного не получается.
B = {1, 2, 3, 6, 7, 14, 21, 42}
A ∩ B = {1, 2, 7, 14}
A ∪ B = {1, 2, 3, 4, 6, 7, 14, 21, 28, 42}