520 в первом, 572 во втором, 440 в третьем
Объяснение:
Пусть x орехов в первом ящике. Во втором ящике на 10% орехов больше, чем в первом, значит количество орехов в нем равно: x + 0,1x = 1,1x В третьем ящике на 80 орехов меньше, чем в первом, и равно: x – 80 При этом во втором ящике на 30% больше, чем в третьем. Составляем уравнение и решаем его: 1,1x = x – 80 + 0,3 ∙ (x – 80) 1,1x = x – 80 + 0,3x – 24 1,1x – x – 0,3x = –80 – 24 –0,2x = –104 x = 520 орехов в первом ящике Тогда во втором ящике: 1,1 ∙ 520 = 572 орехов
Объяснение:
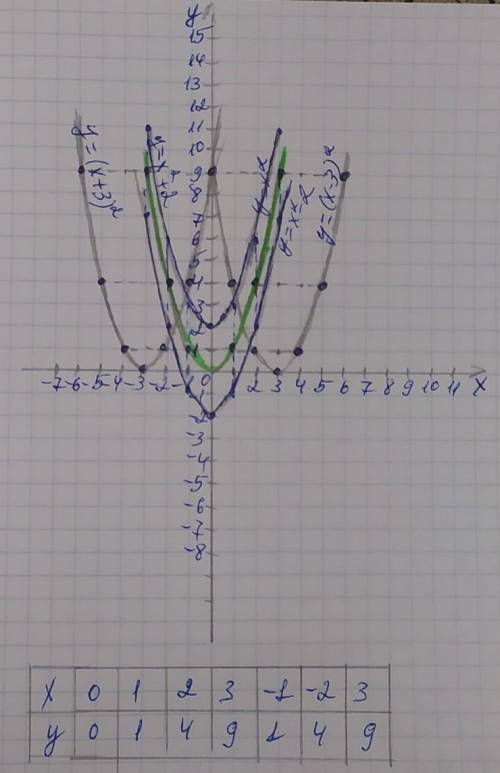
Зелёный график – это исходный у=х²
1) Когда уравнение имеет вид: у=х²–2 исходная парабола спускается вниз по оси у на 2 единицы, поэтому от каждой точки у=х², отсчитывем вниз 2 единицы, соединяем полученные точки и получаем новую параболу
2) у=х²+2
тогда исходная парабола поднимается вверх по оси у на 2 единицы от каждой исходной точки;
3) у=(х–3)²
исходная парабола перемещаться вправо по оси х на 3 единицы от каждой исходной точки;
4) у=(х+3)²
исходная парабола перемещаться влево на 3 единицы от каждой исходной точки.
1 единица=1 клетка
Объяснение:
ДУМАЕМ Площадь фигуры - интеграл разности функций.
Рисунок к задаче в приложении.
РЕШЕНИЕ
1) Находим точки пересечение = пределы интегрирования.
x² - 4*x + 1 = x + 1 превращается в квадратное уравнение:
x²- 5*x = x*(x - 5) = 0
b= 0 - нижний предел и а = 5 - верхний передел интегрирования.
Находим интеграл разности функций: s = 5*x - x² - прямая выше параболы.
S=
Мне нравится именно такая запись решения интеграла - увеличиваем степень и на неё же и делим.
Вычисляем на границах интегрирования.
S(5) = 62 1/2 - 41 2/3 = 20 5/6, S(0) = 0.
S = S(5) - S(0) = 20 5/6 - площадь фигуры - ОТВЕТ (≈ 20,833)