3. Комплект здесяти кон-
вертів і п п'яти листівок кош-
тує 8,5 грн. Скільки коштує
один конверт, якщо два кон-
верти дешевші за три листів-
ки на 50 к

👇

Открыть все ответы

Ответ:

zlatinovaangel

17.04.2021

1)
2^(x-1) -2^(x-6) > 17 ;
(2^(x-6) ) *(2^5 -1) >17 ;
2^(x-6) > 17/31 ;
x-6 > Log_2 17/31 ;
x > 6 +  Log_2  17/31   иначе x∈( 6 +  Log_2  17/31 ;∞) .
---
было бы лучше :
2^(x-1) +2^(x-5) > 17 ;
(2^(x-5))*(2⁴+1) >17
2^(x-5) > 1 ;
2^(x-5) > 2⁰ ;
x-5 > 0 ⇒ x >5 иначе x∈(5 ;∞).

2.
5^(3x) +3*5^(3x-2) < 140 ;
5^(3x-2) * (5² +3) < 140 ;
5^(3x-2) < 5 ;
3x-2 <1   ⇒ x <1 иначе x∈(-∞ ; 1).

ответ :  x∈( - ∞ ;1).

3.
3^(x+2)+3^(x-1) ≤28 ;
3^(x-1)* (3³+1) ≤ 28 ;
3^(x-1)*28  ≤ 28 ;
3^(x-1) ≤ 1 ;
3^(x-1) ≤ 3⁰ ;
x-1 ≤ 0 ;
x ≤ 1  иначе x∈ (-∞ ; 1].

ответ :  x∈( - ∞ ;1].

4,4(42 оценок)

Ответ:

linaaaa2Li

17.04.2021

Объяснение:

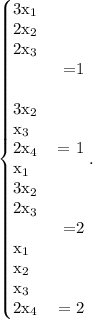
$\left\{\begin{array}{}3x_1&2x_2&2x_3& \ \ \ \ \ \ =1\\&3x_2&x_3&2x_4\ \ =1\\x_1&3x_2&2x_3&\ \ \ \ \ \ \ \ =2\\x_1&x_2&x_3&2x_4\ \ \ =2\end{array}\right..$

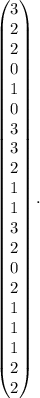
$\left(\begin{array}{}3&2&2&0&1\\0&3&3&2&1\\1&3&2&0&2\\ 1&1&1&2&2\end{array}\right).$

Поменяем местами 1-ю и 3-ю строки:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 1&1&1&2&2\end{array}\right).$

Вычитаем из 4-й строки 1-ю строку:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\3&2&2&0&1\\ 0&-2&-1&2&0\end{array}\right).$

Вычитаем из 3-й строки 1-ю строку, умноженную на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&3&3&2&1\\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Разделим 2-ю строку на 3:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&-7&-4&0&-5\\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 3-ю и 2-ю строку, умноженную на 7:

$\left(\begin{array}{}1&3&2&0&2\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 1-ю и 2-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&-2&-1&2&0\end{array}\right).$

Суммируем 4-ю и 2-ю строку, умноженную на 2:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&3&\frac{14}{3} &-\frac{8}{3} \\ 0&0&1&\frac{10}{3} &\frac{2}{3} \end{array}\right).$

Поменяем местами 4-ю и 3-ю строки:

$\left(\begin{array}{}1&0&-1&-2&1\\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 3-ю и 1-ю строки:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&1&\frac{2}{3} &\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 2-ю и 3-ю строку, умноженную на -1:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&3&\frac{14}{3} &-\frac{8}{3} \end{array}\right).\\$

Суммируем 4-ю и 3-ю строку, умноженную на -3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&-\frac{16}{3} &-\frac{14}{3} \end{array}\right).\\$

Разделим 4-ю строку на -16/3:

$\left(\begin{array}{}1&0&0&\frac{4}{3} &\frac{5}{3} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$

Суммируем 1-ю и 4-ю строку, умноженную на -4/3:

$\left(\begin{array}{}1&0&0&0 &\frac{1}{2} \\0&1&0&-\frac{8}{3} &-\frac{1}{3} \\0&0&1&\frac{10}{3} &\frac{2}{3} \\ 0&0&0&1 &\frac{7}{8} \end{array}\right).\\$